Question

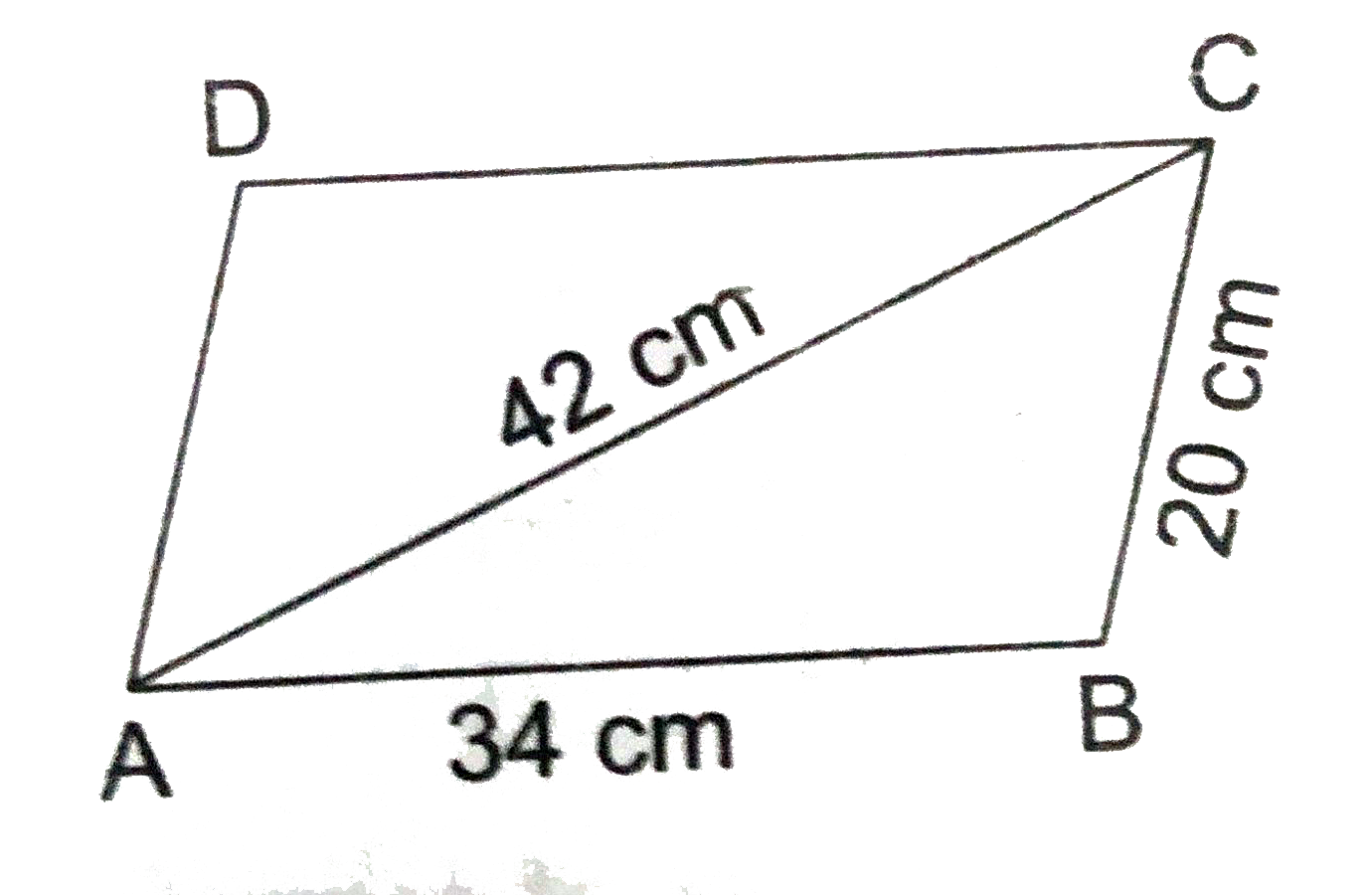
The adjacent sides of a parallelogram $ABCD$
measure $34$ cm and$20$ cm ,
and the diagonal $AC$
measures $42$ cm
Find the area of the parallelogram.

Explanation

To find the area of the parallelogram $$ABCD$$ with adjacent sides measuring $$34$$ cm and $$20$$ cm, and diagonal $$AC$$ measuring $$42$$ cm, we can use Heron's formula. Here’s the step-by-step solution:

Step 1: Identify the sides of the triangles
The diagonal \( AC \) divides the parallelogram into two triangles, \( \triangle ABC \) and \( \triangle ADC \). The sides of triangle \( ABC \) are:
- \( AB = 34 \) cm
- \( BC = 20 \) cm
- \( AC = 42 \) cm

Step 2: Calculate the semi-perimeter \( s \)
The semi-perimeter \( s \) of triangle \( ABC \) is calculated using the formula:
\( s = \frac{AB + BC + AC}{2} \)
Substituting the values:
\( s = \frac{34 + 20 + 42}{2} = \frac{96}{2} = 48 \text{ cm} \)

Step 3: Apply Heron's formula to find the area of triangle \( ABC \)
Heron's formula for the area \( A \) of a triangle is given by:
\( A = \sqrt{s(s-a)(s-b)(s-c)} \)
where \( a, b, c \) are the lengths of the sides of the triangle. Here, \( a = 34 \) cm, \( b = 20 \) cm, and \( c = 42 \) cm.

Substituting the values into the formula:
\( A = \sqrt{48(48-34)(48-20)(48-42)} \)
Calculating each term:
- \( s - a = 48 - 34 = 14 \)
- \( s - b = 48 - 20 = 28 \)
- \( s - c = 48 - 42 = 6 \)

So the area becomes:
\( A = \sqrt{48 \times 14 \times 28 \times 6} \)

Step 4: Simplify the expression under the square root
Calculating the product:
\( A = \sqrt{48 \times 14 \times 28 \times 6} \)
We can simplify this step-by-step:
- First, calculate \( 48 \times 6 = 288 \)
- Then, calculate \( 14 \times 28 = 392 \)
- Now, multiply these results:
\( A = \sqrt{288 \times 392} \)

Step 5: Factor and simplify
To simplify \( 288 \times 392 \):
- \( 288 = 144 \times 2 = 12^2 \times 2 \)
- \( 392 = 196 \times 2 = 14^2 \times 2 \)

Thus:
\( 288 \times 392 = (12^2 \times 2) \times (14^2 \times 2) = 12^2 \times 14^2 \times 4 \)
Taking the square root:
\( A = 12 \times 14 \times 2 = 336 \text{ cm}^2 \)

Step 6: Calculate the area of the parallelogram
Since the area of the parallelogram is twice the area of triangle \( ABC \):
\( \text{Area of parallelogram} = 2 \times 336 = 672 \text{ cm}^2 \)

Final Answer
The area of the parallelogram \( ABCD \) is \( 672 \, \text{cm}^2 \).

---