The adjacent sides of a parallelogram are 6 cm and 8 cm and the angle between them is 30∘ . What is the area of the parallelogram ?
24cm2
12cm2
40cm2
24√3cm2
The correct Answer is:A
To find the area of the parallelogram with adjacent sides of lengths 6 cm and 8 cm, and an angle of 30 degrees between them, we can use the formula for the area of a parallelogram:
Area=base×height=a×b×sin(θ)
where:
- a and b are the lengths of the adjacent sides,
- θ is the angle between the sides.
Step 1: Identify the values
Here, we have:
- a=6 cm (one side)
- b=8 cm (the adjacent side)
- θ=30∘
Step 2: Substitute the values into the formula
Now, substitute the values into the area formula:
Area=6×8×sin(30∘)
Step 3: Calculate sin(30∘)
We know that:
sin(30∘)=12
Step 4: Substitute sin(30∘) into the equation
Now substitute sin(30∘) back into the area formula:
Area=6×8×12
Step 5: Simplify the expression
Now simplify the expression:
Area=6×8×0.5=6×4=24 cm2
Final Answer
Thus, the area of the parallelogram is:
Area=24 cm2
---
- a and b are the lengths of the adjacent sides,
- θ is the angle between the sides.
Here, we have:
- a=6 cm (one side)
- b=8 cm (the adjacent side)
- θ=30∘
Now, substitute the values into the area formula:
We know that:
Now substitute sin(30∘) back into the area formula:
Now simplify the expression:
Thus, the area of the parallelogram is:
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.4
25 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.5
32 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.2
10 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
Knowledge Check
The adjacent sides of a parallelogram are 6 cm and 8 cm and the angle between them is 30∘ . What is the area of the parallelogram ?
A24cm2B12cm2C40cm2D24√3cm2The adjacent sides of parallelogram are 6 cm and 4 cm and the angle between them is 30∘.The area of the parallelogram is -----
A12cm2B24cm2C48cm2DNone of theseTwo adjacent sides of a parallelogram are 12 cm and 9 cm and one of the angle is 30∘ . Find the area of parallelogram.
A27 sq. cmB54 sq. cmC108 sq. cmD96 sq. cm
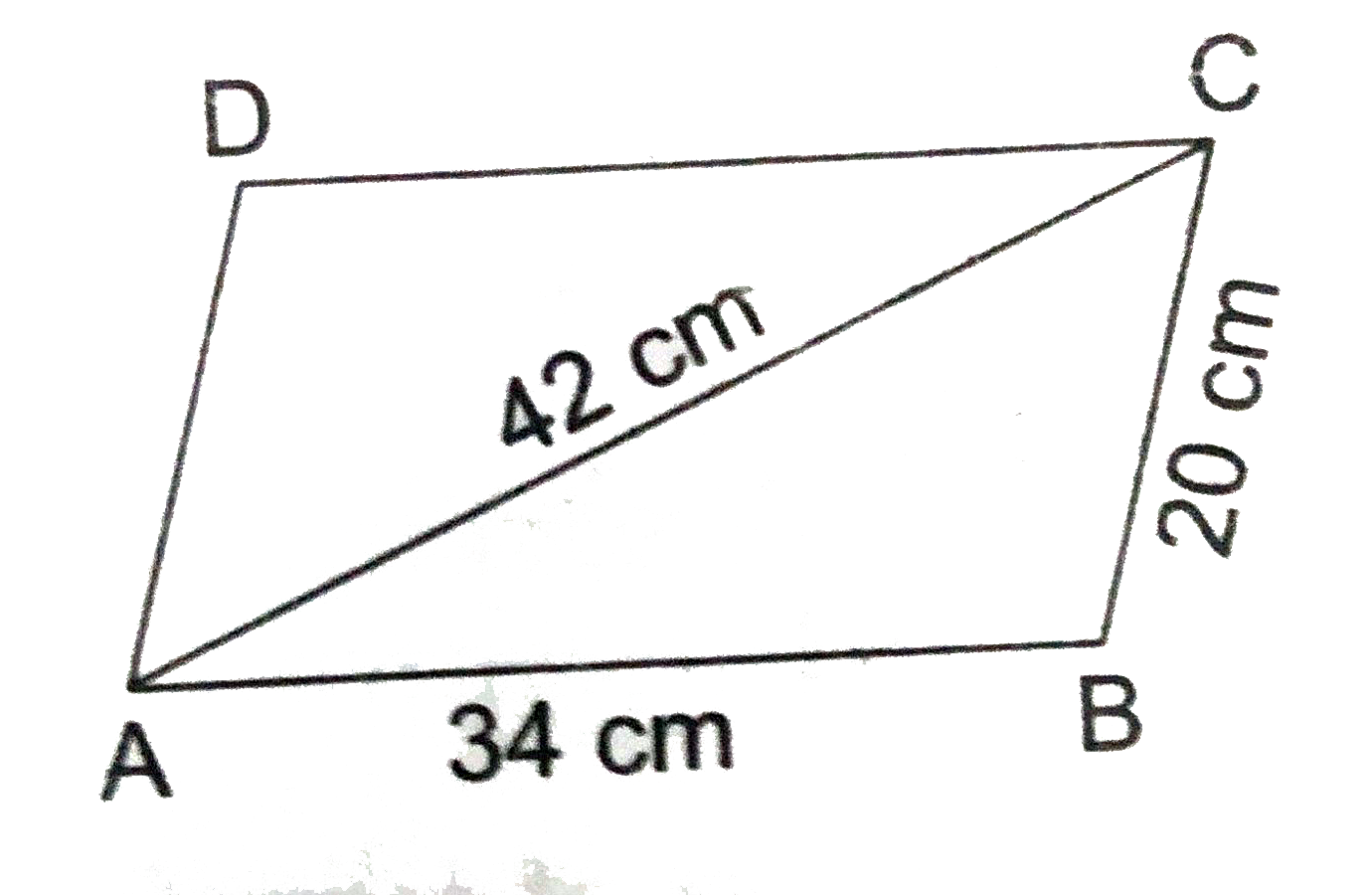
The adjacent sides of a parallelogram ABCD measure 34 cm and20 cm , and the diagonal AC measures 42 cm Find the area of the parallelogram.
View SolutionThe adjacent sides of a parallelogram are 5 cm and 9 cm. Its perimeter is __________.
View SolutionTwo sides of a parallelgram are 12 cm and 8 cm. If one of the interior angles is 135∘, then find area of the parallelogram.
View SolutionThe sum of adjacent angles of a parallelogram is
View SolutionTwo adjacent sides of a parallelogram are 10 cm and 12 cm. If its one diagonal is 14 cm long, find the area of the parallelogram.
View Solution