A spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
inside is zero and varies as outside it
inside is non zero constant and varies as outside it
inside is zero and varies as outside it
inside is constant and varies as outside it
The correct Answer is:C
To find how the electric field varies for a uniformly charged spherical shell, we can apply Gauss's Law. Let's analyze the situation step by step.
1. Understanding the Problem:
We have a spherical shell of radius R with a uniformly distributed charge Q. We need to determine how the electric field E varies inside and outside the shell.
2. Case 1: Inside the Spherical Shell (r<R):
- For any point inside the shell, the enclosed charge Qenclosed is zero because all the charge is on the surface.
- According to Gauss's Law:
∮E⋅dA=Qenclosedϵ0
- Since Qenclosed=0, we have:
∮E⋅dA=0
- This implies that the electric field E inside the spherical shell is:
E=0for r<R
3. Case 2: Outside the Spherical Shell (r>R):
- For points outside the shell, we consider a Gaussian surface of radius r (where r>R).
- The total charge enclosed by this Gaussian surface is Q.
- Applying Gauss's Law:
∮E⋅dA=Qϵ0
- The surface area of the Gaussian sphere is 4πr2, and the electric field E is uniform over this surface:
E⋅4πr2=Qϵ0
- Solving for E:
E=Q4πϵ0r2for r>R
4. Conclusion:
- The electric field inside the spherical shell is zero:
E=0for r<R
- The electric field outside the spherical shell varies inversely with the square of the distance from the center:
E=Q4πϵ0r2for r>R
Summary of Results:
- Inside the shell (r<R): E=0
- Outside the shell (r>R): E∝1r2
We have a spherical shell of radius R with a uniformly distributed charge Q. We need to determine how the electric field E varies inside and outside the shell.
- For any point inside the shell, the enclosed charge Qenclosed is zero because all the charge is on the surface.
- According to Gauss's Law:
∮E⋅dA=Qenclosedϵ0
- Since Qenclosed=0, we have:
∮E⋅dA=0
- This implies that the electric field E inside the spherical shell is:
E=0for r<R
- For points outside the shell, we consider a Gaussian surface of radius r (where r>R).
- The total charge enclosed by this Gaussian surface is Q.
- Applying Gauss's Law:
∮E⋅dA=Qϵ0
- The surface area of the Gaussian sphere is 4πr2, and the electric field E is uniform over this surface:
E⋅4πr2=Qϵ0
- Solving for E:
E=Q4πϵ0r2for r>R
- The electric field inside the spherical shell is zero:
E=0for r<R
- The electric field outside the spherical shell varies inversely with the square of the distance from the center:
E=Q4πϵ0r2for r>R
- Inside the shell (r<R): E=0
- Outside the shell (r>R): E∝1r2
Similar Questions
A spherical shell of radius R carries a uniformly distributed charge q. The electrical forces arising cause the ex-pansion of the shell. Find the mechanical stress in the shell.
View SolutionA spherical shell of radius r carries a uniformly distributed surface charge q on it. A hemispherical shell of radius R(gt r) is placed covering it with its centre coinciding with that of the sphere of radius r. The hemisphere has a uniform surface charge Q on it. The charge distribution on the sphere and the hemisphere is not affected due to each other. Calculate the force that the sphere will exert on the hemisphere.

View Solution
Knowledge Check
A charge Q is uniformly distributed in a dielectric sphere of radius R (having dielectric constant unity). This dielectric sphere is enclosed by a concentric spherical shell of radius 2R and having uniformly distributed charge 2Q. Which of the following graph correctly represents variation of electric field with distance r from the common centre?
 A
A B
B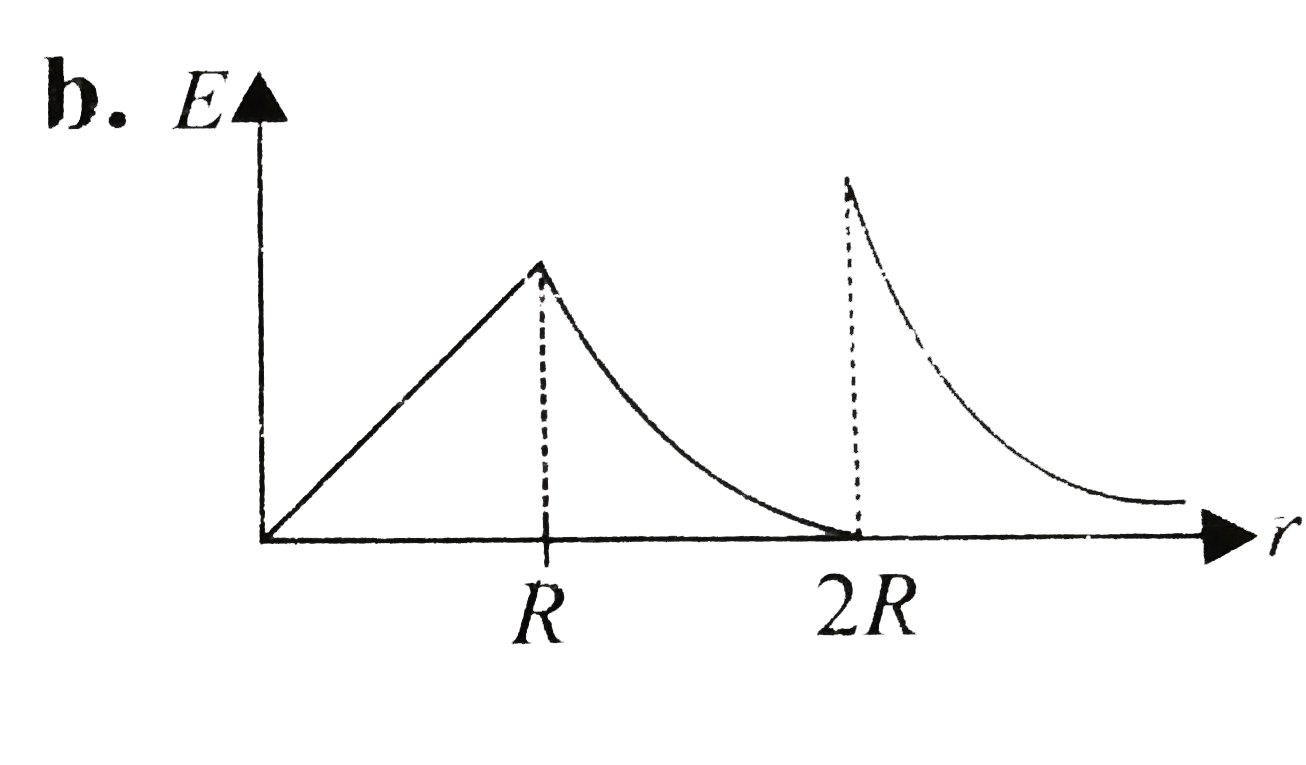 C
C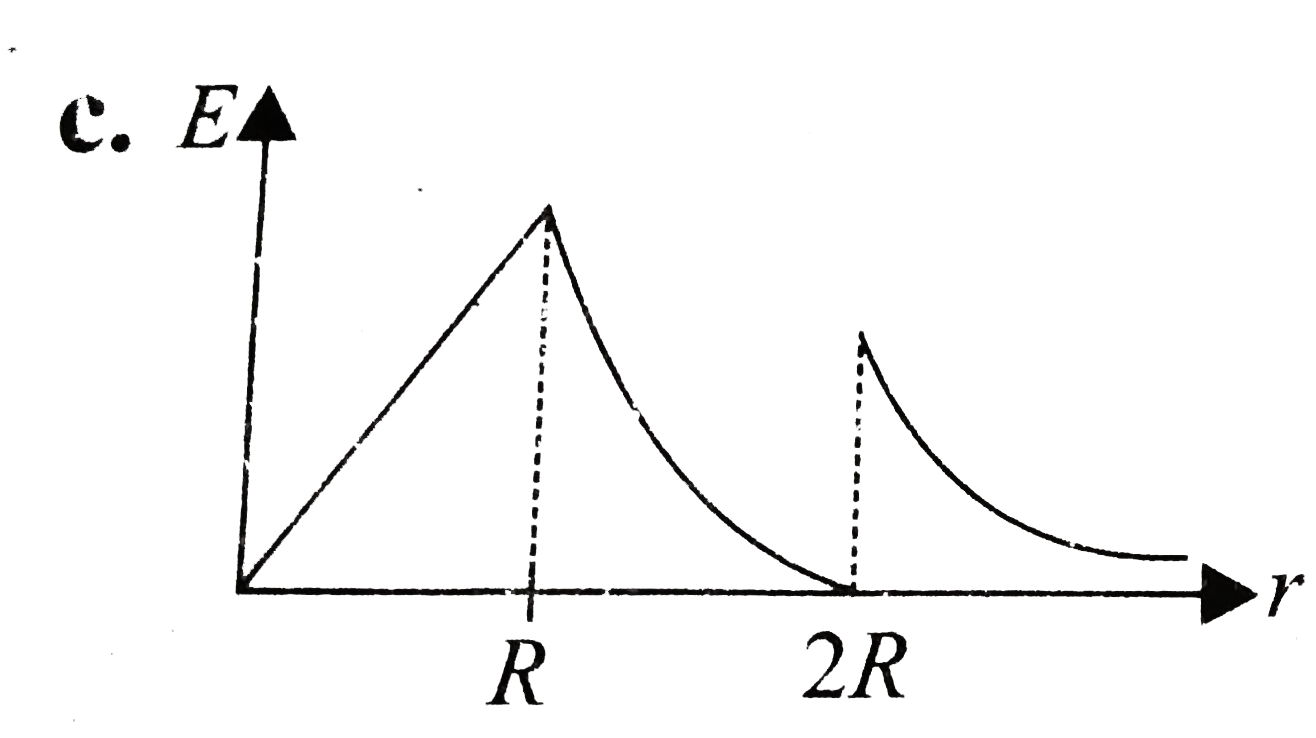 D
D
A spherical shell of radius R has a charge +q units. The electric field due to the shell at a point
Ainside is zero and varies as r−1 outside itBinside is constant and varies as r−2Cinside is zero and varies as r−2 outside itDinside is constant and varies as r−1 outside itA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
AIncreases as r increases for r<Rand for r>RBZero as r increases for r<R, decreases as r increases for r>RCZero as r increases for r<R , increases as r increases for r>RDDecreases as r increases for r<Rand for r>R
A point charge q is placed at a distance d from centre of a uniformly charged conducting spherical shell of radius R and having charge Q as shown. Magnitude of electric field intensity at point P just inside the shell due to charge on shell is
View SolutionA spherical shell having charge +Q (uniformly distributed) and placed as shown. Find the force between shell and the point charge (r>>R).

View SolutionA spherical shell of radius R=1.5cm has a charge q=20μC uniformly distributed over it. The force exerted by one half over the other half is
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionThere is a solid sphere of radius R having uniformly distributed charge throughout it. What is the relation between electric field E and distance r from the centre (r lt R) ?
View Solution
