If the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
4×105NC−1
2×106NC−1
8×107NC−1
12×107NC−1
The correct Answer is:B
To find the electric field intensity at a point 3.6 cm from the axis of a cylinder with a linear charge density of λ=4μC/m, we can use Gauss's law. Here’s a step-by-step solution:
Step 1: Understand the problem
We have a cylinder with a linear charge density λ=4μC/m=4×10−6C/m. We need to find the electric field intensity at a distance r=3.6cm=0.036m from the axis of the cylinder.
Hint: Remember that the electric field due to a uniformly charged cylinder can be derived using Gauss's law.
Step 2: Apply Gauss's Law
Gauss's law states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space ϵ0:
ΦE=Qencϵ0
Step 3: Choose a Gaussian surface
For a cylindrical charge distribution, we choose a cylindrical Gaussian surface of radius r and length h. The electric field E is uniform and directed radially outward.
Step 4: Calculate the charge enclosed
The charge enclosed by the Gaussian surface is given by:
Qenc=λ⋅h
Step 5: Calculate the electric flux
The electric flux through the curved surface of the cylinder is:
ΦE=E⋅(2πrh)
Step 6: Set up the equation using Gauss's Law
From Gauss's law, we equate the electric flux to the charge enclosed divided by ϵ0:
E⋅(2πrh)=λ⋅hϵ0
Step 7: Simplify the equation
We can cancel h from both sides (assuming h≠0):
E⋅(2πr)=λϵ0
Step 8: Solve for E
Now, we can solve for the electric field E:
E=λ2πrϵ0
Step 9: Substitute the values
Substituting the values λ=4×10−6C/m, r=0.036m, and ϵ0=8.85×10−12C2/(N⋅m2):
E=4×10−62π(0.036)(8.85×10−12)
Step 10: Calculate the value
Calculating the denominator:
2π(0.036)(8.85×10−12)≈2.01×10−12
Now substituting back:
E=4×10−62.01×10−12≈1.99×106N/C
Final Result
Thus, the electric field intensity at a point 3.6 cm from the axis of the cylinder is approximately 2×106N/C.
---
We have a cylinder with a linear charge density λ=4μC/m=4×10−6C/m. We need to find the electric field intensity at a distance r=3.6cm=0.036m from the axis of the cylinder.
Gauss's law states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space ϵ0:
For a cylindrical charge distribution, we choose a cylindrical Gaussian surface of radius r and length h. The electric field E is uniform and directed radially outward.
The charge enclosed by the Gaussian surface is given by:
The electric flux through the curved surface of the cylinder is:
From Gauss's law, we equate the electric flux to the charge enclosed divided by ϵ0:
We can cancel h from both sides (assuming h≠0):
Now, we can solve for the electric field E:
Substituting the values λ=4×10−6C/m, r=0.036m, and ϵ0=8.85×10−12C2/(N⋅m2):
Calculating the denominator:
Thus, the electric field intensity at a point 3.6 cm from the axis of the cylinder is approximately 2×106N/C.
Similar Questions
A thin long conductor has linear charge density of 20 μC/m. Calculate the electric field intensity at a point 5 cm from it. Draw a graph to show variation of electric field intensity with distance from the conductor.
View SolutionAn infinitely long cylindrical shell ofinner radius r1 and outer radius r2 is charged in its volume with a volume charge density which varies with distance from axis of cylinder as p=blrC/m3 which C is a positive constant and r is the distance from axis of cylinder. Find the electric field intensity at a point P at a distance x from axis of cylinder
View Solution
Knowledge Check
- Question 1 - Select One
An infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
A0.33×1011N/CB3×1011NC−1C0.66×1011NC−1D1.32×1011NC−1 - Question 2 - Select One
If σ is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is
AσR∈0krBσr∈0kRCσ∈0kDσ2R∈0kr - Question 3 - Select One
A very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformly charged line charge( linear charge density λ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
Aλ=RσBλ=−RσCλ=2πRσDλ=−2πRσ
(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
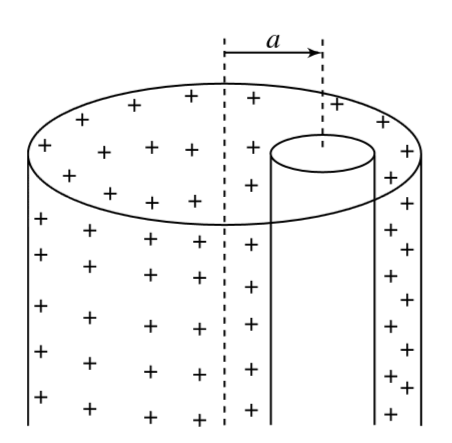 View Solution
View SolutionA plane conductor with very large dimensions is charged such that surface charge density is 1.6×10−2C/m2. The electric field intensity at a point near it if the conductor is in a medium of dielectric constant 5 is
View SolutionFor a point situated at a distance 20 cm from the axis of a long cyclindrical charged conductor, the electric intensity is 0.4N/C . The electric intensity at another point situated at 4o cm from the axis is
View SolutionAn infinitely long uniform linear charge distribution has a charge density 4 μC/m. what is the electric field at a point at a perpendicular distance of 3.6 cm from the line? Given: 14πε0=9×109Nm2/C2
View SolutionFor an infinitely long metal cylinder, the radius is 3 mm, K=6.28 annd charge density=4μC/m2. What is the electric intensity (E) at a distance of 1.5 m from the axis? [14πε0=9×109]
View Solution
