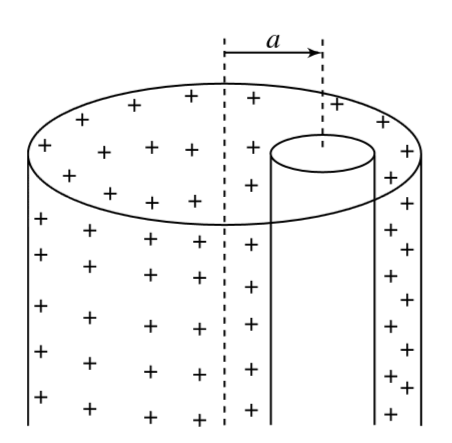
(a) There is a long uniformly charged cylinder having a volume charge density of $ρ C / m^{3}$ . Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.

Text Solution

Verified by Experts

The correct Answer is:(a). (i) $\frac{ρ x}{2 ε_{0} x}$
(ii) $\frac{ρ R^{2}}{2 ε_{0} x}$ field at the surface is maximum
$E_{max} = \frac{ρ R}{2 ε_{0}}$
(b). $\to E = \frac{ρ \to a}{2 ε_{0}}$

Updated on:21/07/2023

A cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
A $E = \frac{1}{4 π \in_{0} K} \cdot \frac{q}{r^{2}}$
B $E = \frac{1}{2 π \in_{0} k} \cdot \frac{q}{r L}$
C $E = σ / \in_{0} k$
Dnone of these
If $σ$ is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is
A $\frac{σ R}{\in_{0} k r}$
B $\frac{σ r}{\in_{0} k R}$
C $\frac{σ}{\in_{0} k}$
D $\frac{σ^{2} R}{\in_{0} k r}$
How does the electric field (E) between the plates of a charged cylindrical capacitor vary with the distance r from the axis of the cylinder ?
A $E \propto \frac{1}{r^{2}}$
B $E \propto \frac{1}{r}$
C $E \propto r^{2}$
D $E \propto r$