Calculate the electrostatic potential energy of two electrons separated by 3 Å in vacuum?
To calculate the electrostatic potential energy (U) of two electrons separated by a distance of 3 Å in a vacuum, we can use the formula for electrostatic potential energy:
U=k⋅q1⋅q2r
Where:
- U = electrostatic potential energy
- k = Coulomb's constant = 9×109N m2/C2
- q1 and q2 = charges of the electrons = −1.6×10−19C
- r = distance between the charges = 3 Å = 3×10−10m
1. Identify the values:
- Charge of an electron, q1=q2=−1.6×10−19C
- Distance, r=3Å=3×10−10m
- Coulomb's constant, k=9×109N m2/C2
2. Substitute the values into the formula:
U=(9×109)⋅(−1.6×10−19)⋅(−1.6×10−19)3×10−10
3. Calculate the numerator:
(−1.6×10−19)⋅(−1.6×10−19)=2.56×10−38
Thus, the numerator becomes:
9×109⋅2.56×10−38=2.304×10−28
4. Calculate the potential energy:
U=2.304×10−283×10−10=7.68×10−19J
5. Convert Joules to electron volts:
To convert Joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
U=7.68×10−191.6×10−19=4.8eV
Final Answer:
The electrostatic potential energy of two electrons separated by 3 Å in vacuum is 4.8eV.
- U = electrostatic potential energy
- k = Coulomb's constant = 9×109N m2/C2
- q1 and q2 = charges of the electrons = −1.6×10−19C
- r = distance between the charges = 3 Å = 3×10−10m
- Charge of an electron, q1=q2=−1.6×10−19C
- Distance, r=3Å=3×10−10m
- Coulomb's constant, k=9×109N m2/C2
U=(9×109)⋅(−1.6×10−19)⋅(−1.6×10−19)3×10−10
(−1.6×10−19)⋅(−1.6×10−19)=2.56×10−38
Thus, the numerator becomes:
9×109⋅2.56×10−38=2.304×10−28
U=2.304×10−283×10−10=7.68×10−19J
To convert Joules to electron volts, we use the conversion factor 1eV=1.6×10−19J:
U=7.68×10−191.6×10−19=4.8eV
The electrostatic potential energy of two electrons separated by 3 Å in vacuum is 4.8eV.
Topper's Solved these Questions
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Chemical Kinetics
30 Videos
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Chemical Equilibrium
38 Videos
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 4 (Level - II) (SUBJECTIVE PROBLEM)
1 Videos
- CLASSROOM PROBLEMS 1BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS 1EXERCISE - THERMODYNAMICS
17 Videos
Similar Questions
Find out the value of electrostatic potential eneryg of two electrons separated by 3.0Å in vacuum. Express your answer in joules and electron volt.
View Solution(a) What is the electric potential energy of two electrons separated by 3.00 nm? (b) If the separation increases, does the potential energy increase or decrease ?
View Solution
Knowledge Check
The electrostatic potential energy between proton and electron separated by a distance 1 Å is
A13.6 eVB27.2 eVC−14.4eVD1.44 eVWhat happens to electrostatic potential energy of a two electron system, if one electrons brought towards another electron?
AIt become zeroBIt decreasesCIt increasesDIt remains sameA proton is nearly 1,836 times more massive than the electron. The Coulomb force of repulsion between two protons separated by a finite distance is F. The electrostatic force between two electrons separated by the same distance is:
AFBF1,837C1,837 FD1,837F
Calculate the electrostatic potential energy for a system of three point charges q placed at the corners of an equilateral triangle of side ‘a’.
View SolutionTwo point charges 4Q, Q are separated by 1m in air. At what point on the line joining the charges is the electric field intensity zero ?
Also calculate the electrostatic potential energy of the system of charges, taking the value of charge, Q=2×10−7C.
View SolutionCalculate the electrostatic potential energy of a system of three point charges q1,q2 and q3 located respectively at →r1,→r2 and →r3 with respect to a common origin O.
View SolutionFind the electrostatic potential energy of the system shown in the figure
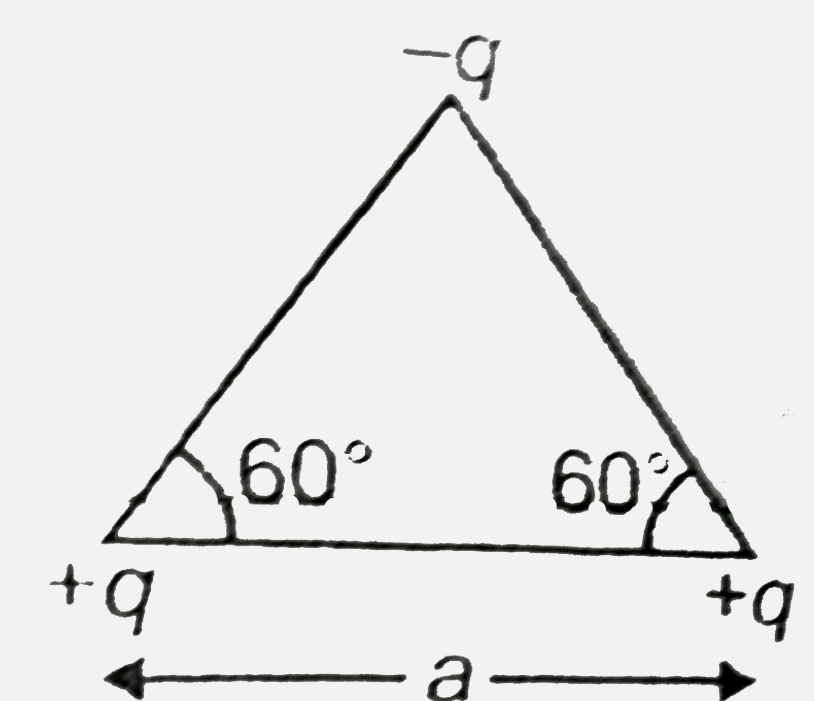
View SolutionTwo point charges 10μCand−10μC are separated by a distance of 40 cm in air.
Calculate the electrostatic potential energy of the system, assuming the zero of the potential energy to be at infinity.
View Solution
