Calculate the electrostatic potential energy of a system of three point charges $q_{1}, q_{2}$ and $q_{3}$ located respectively at ${\to r}_{1}, {\to r}_{2}$ and ${\to r}_{3}$ with respect to a common origin O.

Text Solution

Verified by Experts

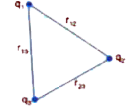
Consider a system of three point charges $q_{1}, q_{2}$ and $q_{3}$ as shown in Fig. The potential energy of a system of point charges is equal to work done in building up this configuration of charges .
To bring $q_{1}$ first from infinity to its present position no work is done because there is no force i.e., $W_{1} = 0$ .
To bring $q_{2}$ from infinity to its present position work is to be done against the electric field of charge $q_{1}$ . By definition this work done is
$W_{2} = q_{2} . V ({\to r}_{2}) = q_{2} . \frac{1}{4 π \in_{0}}, \frac{q_{1}}{r_{12}} = \frac{1}{4 π \in_{0}} \cdot \frac{q_{1} q_{2}}{r_{12}}$
Now to bring $q_{3}$ from infinity to its present position work is to be done against the combined electric fields of $q_{1}$ and $q_{2}$ . Thus ,
$W_{3} = q_{3} [V_{1} ({\to r}_{3}) + V_{2} ({\to r}_{3})] = q_{3} [\frac{1}{4 π \in_{0}} \cdot \frac{q_{1}}{r_{13}} + \frac{1}{4 π \in_{0}} \cdot \frac{q_{2}}{r_{23}}] = \frac{1}{4 π \in_{0}} [\cdot \frac{q_{1} q_{3}}{r_{13}} + + \frac{q_{2} q_{3}}{r_{23}}]$
Thus , total work done in building up the charge configuration $W = W_{1} + W_{2} + W_{3} = \frac{1}{4 π \in_{0}} [\frac{q_{1} q_{2}}{r_{12}} + \frac{q_{1} q_{3}}{r_{13}} + \frac{q_{2} q_{3}}{r_{23}}]$
$∴$ Electrostatic potential energy of the given configuration
$U = \frac{1}{4 π \in_{0}} [\frac{q_{1} q_{2}}{r_{12}} + \frac{q_{1} q_{3}}{r_{13}} + \frac{q_{2} q_{3}}{r_{23}}]$ .

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

In, the charges on $C_{1}, C_{2}$ , and $C_{3}$ , are $Q_{1}, Q_{2}$ , and $Q_{3}$ , respectively.
.
A $Q_{2} = 8 μ C$
B $Q_{3} = 12 μ C$
C $Q_{1} = 20 μ C$
D $Q_{2} = 12 μ C$

U-LIKE SERIES-ELECTROSTATIC POTENTIAL AND CAPACITANCE -LONG ANSWER QUESTIONS-I

Home
Ask Doubt
Profile