For the reaction A ⇔ B, ΔE for the reaction is –33.0 kJ mol–1. Calculate If Ef and Eb are in the ratio 20 : 31, calculate Ef,Eb at 300 K. Assuming pre-exponential factor same for forward and backward reactions.
To solve the problem, we need to calculate the activation energies Ef and Eb for the forward and backward reactions, respectively, given the ratio of Ef to Eb and the enthalpy change ΔE for the reaction.
1. Identify the Given Information:
- The change in energy ΔE=−33.0kJ/mol.
- The ratio of activation energies Ef:Eb=20:31.
2. Express Activation Energies in Terms of a Variable:
- Let Ef=20x and Eb=31x.
3. Use the Relationship between Activation Energies and Enthalpy Change:
- The relationship between the forward and backward activation energies and the enthalpy change is given by:
Ef−Eb=ΔH
- Substituting the expressions for Ef and Eb:
20x−31x=−33.0kJ/mol
- This simplifies to:
−11x=−33.0kJ/mol
4. Solve for x:
- Dividing both sides by -11:
x=33.011=3.0
5. Calculate Ef and Eb:
- Now substitute x back to find Ef and Eb:
Ef=20x=20×3=60.0kJ/mol
Eb=31x=31×3=93.0kJ/mol
Final Results:
- Ef=60.0kJ/mol
- Eb=93.0kJ/mol
- The change in energy ΔE=−33.0kJ/mol.
- The ratio of activation energies Ef:Eb=20:31.
- Let Ef=20x and Eb=31x.
- The relationship between the forward and backward activation energies and the enthalpy change is given by:
Ef−Eb=ΔH
- Substituting the expressions for Ef and Eb:
20x−31x=−33.0kJ/mol
- This simplifies to:
−11x=−33.0kJ/mol
- Dividing both sides by -11:
x=33.011=3.0
- Now substitute x back to find Ef and Eb:
Ef=20x=20×3=60.0kJ/mol
Eb=31x=31×3=93.0kJ/mol
- Ef=60.0kJ/mol
- Eb=93.0kJ/mol
Topper's Solved these Questions
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Chemical Equilibrium
38 Videos
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Radioactivity
23 Videos
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Electrochemistry
22 Videos
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 4 (Level - II) (SUBJECTIVE PROBLEM)
1 Videos
- CLASSROOM PROBLEMS 1BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS 1EXERCISE - THERMODYNAMICS
17 Videos
Similar Questions
For the reaction A ⇔ B, ΔE for the reaction is –33.0 kJ mol–1. Calculate equilibrium constant KC for the reaction at 300 K
View SolutionFor the reaction,
A⇔B,δH for the reaction is -33.0 kJ/mol.
Calculate
(i) Equilibrium constant Kc for the reaction at 300 K
(ii) If Ea(f)andEa(r) in the ratio 20:31 , calculate Ea(f) at 300 K .
Assuming pre-exponential factor same for forward and reverse reaction.
View Solution
Knowledge Check
The energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1.

Assuming that pre-exponential factor is same for forward and backward reaction answer the following:
The energy of activation for forward and backward reactions (Ef and Eb) at 300K. Given that Ef and Eb are in the ratio 20:31,A69,93B60,93C93,60D90,60The Ea for forward reaction is 50 kcal. The Ea for its backward reaction is:
Aequal 50 kealBgreater than 50 kealCless than 50Dless than 50
The energy change accompanying the equilibrium reaction A ⇔ B is −33.0 kJ mol−1. Calculate
(i) Equilibrium constant Kc for the reaction at 300 K
(ii) Energy of activation for forward and backward reaction (Ef and Eb) at 300 K. Given that Ef and Eb are in the ratio 20 : 31.
Assume that pre-exponential factor is same for forward and backward reaction.
View SolutionThe energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1. Calculate Energy of activation for forward and backward reaction (EfandEa) at 300 K. Given that EfandEb are in the ratio 20 : 31. Assume that pre-exponential factor is same for forward and backward reaction.
View SolutionFor a reversible reaction C⇔D, heat of reaction at constant volume is −33.0kJmol−1, calculate:
(i) The equilibrium constant at 300K.
(ii) If Ef and Eb are energy of activation for forward and backward reactions respectively, calculate Ef and Eb at 300K. Given that Ef:Eb=20:31 Assumw pre exponential factor same for forward and backward reaction.
View SolutionThe energy change accompanying the equilibrium reaction A⇔B is −33.0kJmol−1. Calculate Equilibrium constant Ka for the reaction at 300 K
View SolutionFrom the following data for the reaction between A and B
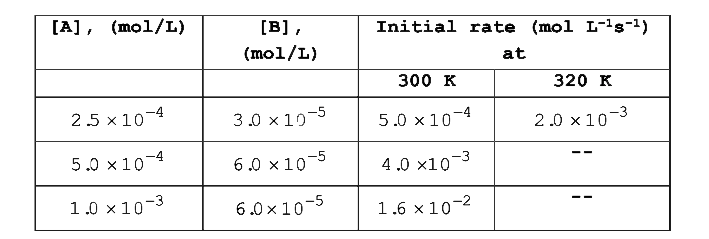
Calculate:
(i) the order of the reaction with respect to A and with respect to B
(ii) the rate constant at 300 K
(iii) the pre-exponential factor.
View Solutionform the following data for the reaction between A and B,

(a) Calculate the order of the reaction with respect to A and with respect to B.
(b) Calculate the rate constant at 300K.
( c) Calculate the pre-expontential factor.
View Solution
