For a reaction, if effective rate constant k' is given b
k=2k2k3(k1k5)1/5
where k1,k2,k3,k5 are rate constants for different steps of the reaction
The effective activation energy is
E'a=Ea2−Ea3+15Ea1−15Ea5
E'a=Ea1+Ea2+Ea3+Ea5
E'a=Ea1+Ea2−Ea3−Ea5
E'a=Ea2+Ea3−Ea5−Ea1
To find the effective activation energy (Ea) for the given reaction, we start with the provided equation for the effective rate constant k′:
k=2k2k3(k1k5)15
Step 1: Apply the Arrhenius Equation
The Arrhenius equation relates the rate constant k to the activation energy Ea:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the gas constant,
- T is the temperature.
Step 2: Take the Natural Logarithm
Taking the natural logarithm of both sides gives:
ln(k)=ln(A)−EaRT
Step 3: Substitute the Effective Rate Constant
Substituting k′ into the equation, we have:
ln(k′)=ln(2k2k3)+15ln(k1k5)
Step 4: Expand the Logarithm
Using properties of logarithms, we can expand this:
ln(k′)=ln(2)+ln(k2)−ln(k3)+15(ln(k1)−ln(k5))
Step 5: Relate to Activation Energies
Now, we can relate the logarithmic terms to their respective activation energies:
ln(k2)=ln(A2)−Ea2RT
ln(k3)=ln(A3)−Ea3RT
ln(k1)=ln(A1)−Ea1RT
ln(k5)=ln(A5)−Ea5RT
Step 6: Substitute Activation Energies
Substituting these into the equation for ln(k′):
ln(k′)=ln(2)+(ln(A2)−Ea2RT)−(ln(A3)−Ea3RT)+15(ln(A1)−Ea1RT−ln(A5)+Ea5RT)
Step 7: Combine Terms
Combining the terms, we can isolate the effective activation energy Ea:
ln(k′)=ln(2)+ln(A2)−ln(A3)+15(ln(A1)−ln(A5))−⎛⎝Ea2−Ea3+15(Ea1−Ea5)RT⎞⎠
Step 8: Identify Effective Activation Energy
From this, we can identify the effective activation energy Ea:
Ea=Ea2−Ea3+15(Ea1−Ea5)
Final Answer
Thus, the effective activation energy for the reaction is:
Ea=Ea2−Ea3+15(Ea1−Ea5)
The Arrhenius equation relates the rate constant k to the activation energy Ea:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the gas constant,
- T is the temperature.
Taking the natural logarithm of both sides gives:
Substituting k′ into the equation, we have:
Using properties of logarithms, we can expand this:
Now, we can relate the logarithmic terms to their respective activation energies:
ln(k3)=ln(A3)−Ea3RT
ln(k1)=ln(A1)−Ea1RT
ln(k5)=ln(A5)−Ea5RT
Substituting these into the equation for ln(k′):
Combining the terms, we can isolate the effective activation energy Ea:
From this, we can identify the effective activation energy Ea:
Thus, the effective activation energy for the reaction is:
Topper's Solved these Questions
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Chemical Equilibrium
38 Videos
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Radioactivity
23 Videos
- CLASSROOM PROBLEMS BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS EXERCISE - Electrochemistry
22 Videos
- Chemical KineticsBOOK - MOTIONCHAPTER - Chemical KineticsEXERCISE - Exercise - 4 (Level - II) (SUBJECTIVE PROBLEM)
1 Videos
- CLASSROOM PROBLEMS 1BOOK - MOTIONCHAPTER - CLASSROOM PROBLEMS 1EXERCISE - THERMODYNAMICS
17 Videos
Similar Questions
For a reaction, if effective rate constant k' is given b
k=2k2k3(k1k5)1/5
where k1,k2,k3,k5 are rate constants for different steps of the reaction
The effective frequency factor
View SolutionFor a reaction, if effective rate constant k' is given b
k=2k2k3(k1k5)1/5
where k1,k2,k3,k5 are rate constants for different steps of the reaction
Which one is correct ?
View Solution
Knowledge Check
A reaction is represented by A→k1B (slow).
A+B→k2C (fast). Where k1andk2 are the rate constants of the mechanistic steps. The rate of production of C will be given byAk1[A][B]Bk1[A]Ck1k2[A]DK2[A][B]A reaction takes place in various steps. The rate constatn for first, second, third and fifth steps are k1,k2,k3 and k5 respectively The overall rate constant is given by
k=k2k3(k1k5)1/2
If activation energy are 40, 60, 50, and 10 kJ/mol respectively, the overall energy of activation (kJ/mol) is :A10B20C25Dnone of theseA reaction is represented by Ak1−−→B (slow ) and A+Bk2−−→C (fast) where k1 and k2 are the ratge constants of two steps. The rate of production of C will be given by
Ak1[A][B]Bk1[A]Ck1k2[A]Dk2[A][B]
A reaction takes place in various steps. The rate constant for first, second, third and fifth steps are k1, k2, k3 and k5 respectively. The overall rate constant is is given by:
k=k2k1(k1k2)12 activation energy are 40,60, 50 and 10 kJ/mol respectively, find the overall energy of activation (kJ/mol).
View Solution60.A consecutive reaction occurs with two equilibria which co-exist together Pk1k2Qk3k4R Where k1,k2,k3 and k4 are rate constants.Then the equilibrium constant for the reaction P ↔ R is
(1) (k1⋅k2)/(k3⋅k4)
(2) (k1⋅k4)/(k2k3)
(3) k1*k2*k3⋅k4
(4) (k1⋅k3)/(k2k4)]]
View SolutionA reaction is represented by :
A→B slow and A+B→C (fast) where k1andk2 are the rate constants of the mechanistic steps. The rate of production of B will be given by :
View SolutionFor the reaction
(i) AkI−−→P
(ii) BKII−−→Q, following observation is made.
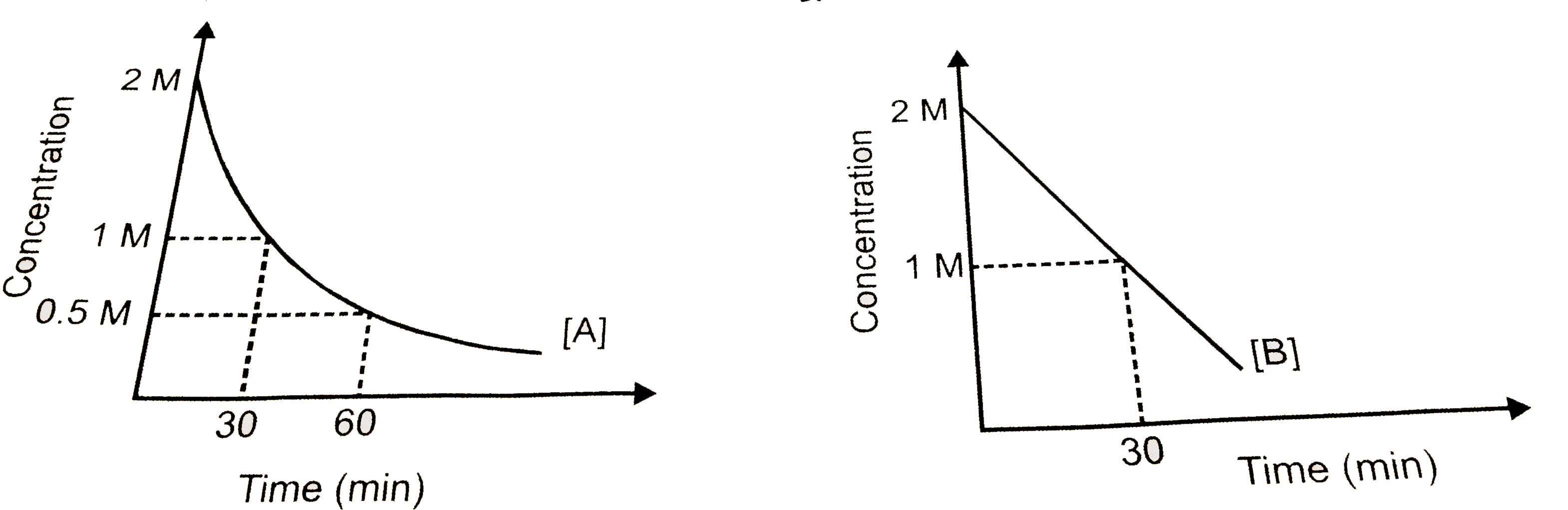
Calculate k1kII, where kI and kII and rate constant for the respective reaction.
View SolutionK1 and K2 are the rate constants of forward and backward reactions. The equilibrium constant K of the reaction is -
View Solution
