A face-centred cubic solid of an element A has a largest sized guest atom B at the body centre octahedral hole if insertion of B doesn't affect the original unit cell dimension, determine the packing fraction of the solid.

Text Solution

Verified by Experts

In the given solid, there is one B and four A per unit cell.

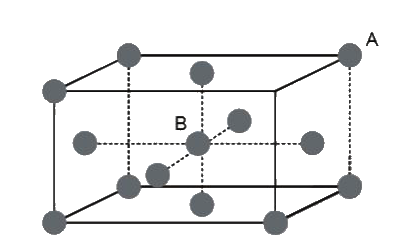
Also, under the condition of largest possible size of B, it will be in contact of A present at the face centres only and the following relatinship will exist : $4 r_{A} \sqrt{2}$ and $2 (r_{A} + r_{B}) = a$
solving $\frac{r_{B}}{r_{A}} = 0.414$
Now,packing fraction
$(ϕ) = \frac{4 π}{3} (4 r_{A}^{3} + r_{B}^{3}) \times \frac{1}{a^{3}} = \frac{4 π}{3} (4 r_{A}^{3} + r_{B}^{3}) \times \frac{1}{1 \sqrt{2 r_{A}^{3}}}$
$\frac{π}{12 \sqrt{2}} [4 + {(\frac{r_{B}}{r_{A}})}^{3}] = \frac{π}{12 (\sqrt{2})} [4 + {(0.414)}^{3}] = 0.7536$

Updated on:21/07/2023

A cubic solid is made up of two elements A and B are present at the corners of the cube and atoms A at the body centre predict the formula of the compound
A $A B_{2}$
BAB
C $A_{2} B$
Dnone of the above
In a face-centred cubic arrangement of A and B atoms, A atoms are at the corners of the unit cell and B atoms at the face centres. One of the A atoms is missing from one corner in the unit cell. The simplest formula of the compound is
A $A_{7} B_{3}$
B $A B_{3}$
C $A_{7} B_{24}$
D $A_{7 / 8} B_{5}$
A face-centred cubic lattice of a single type of atoms has same defects and its one corner and one face centre is left unoccupied per unit cell. Calculate the packing fraction of such solid.
A0.325
B0.256
C0.625
D0.312