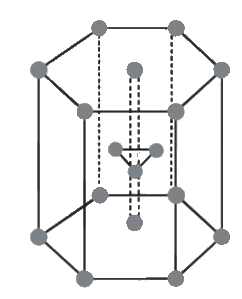
An atom crystallises in hexogonal closed pack arrangement. Determine dimensions (radius and length) of a large cyclindrical atom that can be accommodated in the centre of HCP, in terms of radius of host atom.

Text Solution

Verified by Experts

The cylinder will pass through centre of middle layer and will lie between the face centres. Therefore, Height of cylinder (h) = height of hexagon (h) = 2r
Since ,in HCP:H= $4 = \sqrt{\frac{2}{3}} r$ ,
Where r= radius of atoms.
$\Rightarrow h = (4 \sqrt{\frac{2}{3} - 2}$ r=1.266 r
Also, if R is the radius of cylinder, then in the case of closet contact : $\frac{R}{r} = 0.155 \Rightarrow R = 0.155 r, \Rightarrow h = 1.266 r$

Updated on:21/07/2023

Silver metal crystallises in a cubic closed packed arrangement with edge length 404 pm .Thus radius of the silver atom is
A $203.5$ pm
B $138.8$ pm
C $142.8$ pm
D $407.0$ pm
Aluminium crystallises in a cubic close-packed structure. Radius of the atom in the metal is 125 pm.
What is the length of the side of the unit cell?
A354 pm, 2.254 x $10^{22}$ unit cells
B254 pm, 3.254 x $10^{22}$ unit cells
C454 pm, 4.254 x $10^{22}$ unit cells
D654 pm, 5.254 x $10^{22}$ unit cells
Arrange the following atoms in the ascending order of atomic radius
AF,Cl,O,C
BC,O,F,Cl
CO,C,F,Cl
DF,O,C,Cl