In figure, a dart is thrown and lands n the interior of the circle. What is the probability that the dart will land in the shaded region?
A dart is thrown and lands in the interior of the circle.
Probability that it will land in the shaded region = (area of shaded region)/(area of circle)
We will need to find the radius of circle.
Clearly, diagonal of the rectangle = diameter of the circle.
By Pythagoras theorem, we can calculate diagonal of the rectangle
diagonal =10units
Now, this means
diameter =10units
radius =5units
So, area of circle=πr2=(5)2π sq. units.
=25π sq. units
And, area of shaded region = area of circle - area of rectangle
area of rectangle =l×b=6×8=48 sq. units
So area of shaded region=25π−48
Taking πas3.14, we get
25(3.14)−48=78.5−48=30.5 sq. units
So , probability =30.578.5=61157
Topper's Solved these Questions
Similar Questions

In figure, a dart is thrown and lands in the interior of the circle.
What is the probability that the dart will land in the shaded region ?View Solution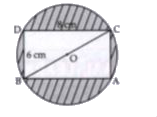
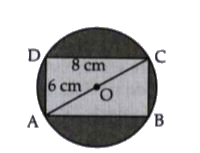
In figure, a dart is thrown and lands in the interior of the circle.
What is the probability that the dart will land in rectangle ABCD region ?View SolutionIn the adjoining figure a dart is thrown at the dart board and lands in the interior of the circle . What is the probability that the dart will land in the shaded region.
 View Solution
View Solution
In figure, a dart is thrown and lands in the interior of the circle.
Find the area of the circle.View Solution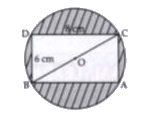
In figure, a dart is thrown and lands in the interior of the circle.
Find the area of rectangle ABCD.View Solution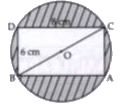
In figure, a dart is thrown and lands in the interior of the circle.
Find the area of right triangle ABC.View SolutionA target shown in Figure, consists of three concentric circles of radii 3,7 and 9cm respectively. A dart is thrown and lands on the target. What is probability that the dart will and on the shaded region?
View SolutionIn the Figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square?
View SolutionIn the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
View SolutionWhat is probability of the spinner landing on Rs 100
 View Solution
View Solution

