In ABC , the bisector of ∠B meets AC at D. A line PQAC meets AB,BCandBD at P,QandR respectively, Show that PR.BQ=QR.BP (ii) ABxCQ=BCxAP
Step by step video & image solution for In A B C , the bisector of /_B meets A C at Ddot A line P Q A C meets A B , B Ca n dB D at P ,Qa n dR respectively, Show that P RdotB Q=Q RdotB P (ii) A BxC Q=B CxA P by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn the figure bisector of ∠B & ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that
∠P+∠Q=12(∠ABC+∠ADC).
View SolutionIn ABC and PQR Figure, AB=PQ,BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX =∠PQY. Prove that ABC≅PQR. Figure
View SolutionIn Figure, bisectors of ∠B and ∠D of quadrilateral ABCD meet CD and AB produced at P and Q respectively. Prove that ∠P+∠Q=12(∠ABC+∠ADC).
View SolutionTwo triangle ABC and DBC lie on the same side of the base BC . From a point P on BC,PQAB AND PRBD ARE DRAWN. They meet AC in Q and DC in R respectively. Prove that QRAD.
View SolutionIn a triangle ABC , let PandQ be points on ABandAC respectively such that PQ∣∣BC . Prove that the median AD bisects PQ.
View SolutionThe pth, qth and rth terms of an A.P. are a, b and c respectively. Show that a(q – r) + b(r-p) + c(p – q) = 0
View SolutionIn Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD
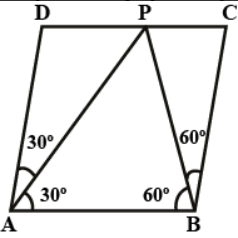
View SolutionAn exterior angle of a triangle is 1100 , and one of the interior opposite angles is 300. Find the other two angles of the triangle.
View SolutionThe sides AB and AC of a ABC are produced to P and Q respectively. If the bisectors of ∠PBC AND ∠QCB intersect at O, then ∠BOC=900−12∠A GIVEN : A ABC in which sides AB and AC are produced to P and Q respectively. The bisectors of ∠PBC and ∠QCB intersect at O.
View Solution
