ABCD is a parallelogram. P is a point on the side BC DP when produced meets AB produced at L. Prove that DPPL=DCBL (ii) DLDP=ALDC
To prove the statements given in the question, we will use the properties of parallelograms and the concept of similar triangles.
Given:
- ABCD is a parallelogram.
- P is a point on side BC.
- DP when produced meets AB produced at L.
To Prove:
1. DPPL=DCBL
2. DLDP=ALDC
Step 1: Identify the triangles
In triangle ADL, since AD is parallel to BC (property of parallelogram), we can apply the Basic Proportionality Theorem (also known as Thales' theorem).
Step 2: Apply the Basic Proportionality Theorem
According to the theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Thus, we have:
LBBA=LDDP
Step 3: Substitute equal lengths
Since AB=DC (opposite sides of a parallelogram are equal), we can replace AB with DC:
LBDC=LDDP
Step 4: Rearranging the equation
From the above equation, we can rearrange it to find the ratio we need:
DPPL=DCBL
This proves the first part of the question.
Step 5: Prove the second part
Now, we need to prove that:
DLDP=ALDC
From the previous step, we have:
DPPL=DCBL
Step 6: Express DL in terms of DP
To express DL in terms of DP, we can add PL to both sides of the equation:
PL+DPDP=BL+DCDC
Step 7: Recognize total lengths
Notice that AL=AB+BL and since AB=DC, we can write:
AL=DC+BL
Step 8: Substitute and simplify
Now substituting this back into our equation gives:
DLDP=ALDC
This completes the proof for the second part.
Conclusion
Thus, we have proved both parts of the question:
1. DPPL=DCBL
2. DLDP=ALDC
- ABCD is a parallelogram.
- P is a point on side BC.
- DP when produced meets AB produced at L.
1. DPPL=DCBL
2. DLDP=ALDC
In triangle ADL, since AD is parallel to BC (property of parallelogram), we can apply the Basic Proportionality Theorem (also known as Thales' theorem).
According to the theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Thus, we have:
Since AB=DC (opposite sides of a parallelogram are equal), we can replace AB with DC:
From the above equation, we can rearrange it to find the ratio we need:
Now, we need to prove that:
To express DL in terms of DP, we can add PL to both sides of the equation:
Notice that AL=AB+BL and since AB=DC, we can write:
Now substituting this back into our equation gives:
Thus, we have proved both parts of the question:
2. DLDP=ALDC
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. P is a point on the side BC DP when produced meets AB produced at L. Prove that DPPL=DCBL (ii) DLDP=ALDC
View SolutionABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionIn the adjoining figure, ABCD is a parallelogram and E is the midpoint of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L. Prove that (i) AF=2DC, (ii) DF=2DL
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM . Prove that LM and BD bisect each other.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R. Prove that R is a mid-point of BC.
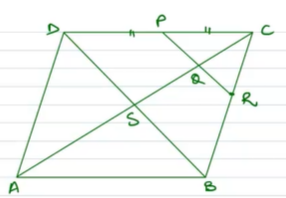
View SolutionABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionIn Figure, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ=14AC. If PQ produced meets BC at R, prove that R is a mid-point of BC
View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
View Solution
