ABCandPQR are similar triangles such that ∠A=320 and ∠R=650. Then, ∠Q is 830 (b) 320 (c) 650 (d) 970
To find the measure of angle Q in the similar triangles ABC and PQR, we can follow these steps:
Step 1: Identify the given angles
We are given:
- Angle A = 32°
- Angle R = 65°
Step 2: Use the property of similar triangles
Since triangles ABC and PQR are similar, the corresponding angles are equal. Therefore:
- Angle A = Angle P = 32°
- Angle R = Angle C = 65°
Step 3: Use the triangle sum property
The sum of the angles in any triangle is 180°. For triangle PQR, we can write:
Angle P+Angle Q+Angle R=180°
Substituting the known values:
32°+Angle Q+65°=180°
Step 4: Simplify the equation
Combine the known angles:
97°+Angle Q=180°
Step 5: Solve for angle Q
Now, isolate Angle Q:
Angle Q=180°−97°
Angle Q=83°
Conclusion
Thus, the measure of angle Q is 83°.
We are given:
- Angle A = 32°
- Angle R = 65°
Since triangles ABC and PQR are similar, the corresponding angles are equal. Therefore:
- Angle A = Angle P = 32°
- Angle R = Angle C = 65°
The sum of the angles in any triangle is 180°. For triangle PQR, we can write:
Angle P+Angle Q+Angle R=180°
Substituting the known values:
32°+Angle Q+65°=180°
Combine the known angles:
97°+Angle Q=180°
Now, isolate Angle Q:
Angle Q=180°−97°
Angle Q=83°
Thus, the measure of angle Q is 83°.
Topper's Solved these Questions
Similar Questions
In Figure, chords AD and BC intersect each other at right angles at a point P. If ∠DAB=350, then ∠ADC= 350 (b) 450 (c) 550 (d) 650
View SolutionLine segments AB and CD intersect at O such that AC∣∣DB. If ∠CAB=450and ∠CDB=550, then ∠BOD= 1000 (b) 800 (c) 900 (d) 1350
View SolutionIn Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View SolutionABC is an isosceles triangle such that AB=ACandAD is the median to base BC . Then, ∠BAD=
(a) 55∘
(b) 70∘
(c) 35∘
(d) 110∘
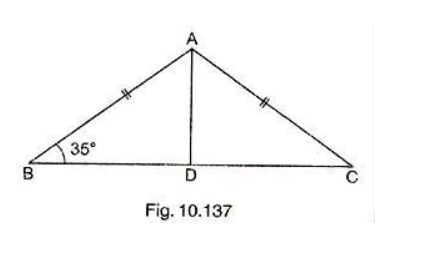 View Solution
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View SolutionIn Fig.92, AOB is a straight line such that ∠AOC=(3x+10)0, ∠COD=500 and ∠BOD=(x−8)0. The value of x is (a) 32 (b) 36 (c) 42 (d) 52
View SolutionThe diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD=50∘, then ∠DPC= 70∘ (b) 90∘ (c) 80∘ (d) 100∘
View SolutionIn Figure, PQ∣∣RS, ∠AEF=950, ∠BHS=1100 and ∠ABC=x0. Then the value of x is (a)150 (b) 250 (c) 700 (d) 350
View SolutionIn Fig. 74, a transversal n cuts two lines l and m such that ∠2=650 and ∠8=650. Are the lines parallel?
View SolutionIf A and B are two events such that P(A∩B)=0.32 and P(B)=.5,thenP(A/B)
View Solution

