A long horizontal glass capillary tube open at both ends contains a mercury thread 1 m long at . Find the length of the mercury thread, as read on this scale, at .
The correct Answer is:1.0154 m
Step by step video, text & image solution for A long horizontal glass capillary tube open at both ends contains a mercury thread 1 m long at 0^@C. Find the length of the mercury thread, as read on this scale, at 100^@C. (gamma_("mercury")=18.2xx10^-5K^-1alpha_("glass")=9xx10^-6K^-1) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - ADVANCE MCQs WITH ONE OR MORE OPTIONIS CORRECT24videos
HEAT AND THERMAL EXPANSION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO66videos
HEAT TRANSFER
Similar Questions
A long horizontal glass capillary tube open at both ends contains a mercury thread 1m long at 00C. A scale is etched on the glass tube. This scale is correct at 00C. Find the length of mercury thread as shown by this scale at 1000C. Also find original length of thread at 00C. ( gamma_mercury = 18.2 x 10^-5 K^-1, alpha_glass = 9 x 10^-6 K ^-1)
View SolutionA vertical glass tube,closed at the bottom contains mercury to a height of 100cm at 30∘C , The height of mercury column at 50∘C is (γforHg=1.8×10−4^(∘)C,αg=8×10−6^(∘)C)
View Solution
Knowledge Check
- Question 1 - Select One
A glass flask of volume 200cm3 is just filled with mercury at 20∘C. The amount of mercury that will overflow when the temperature of the system is raised to 100∘C is (γglass=1.2×10−5/C∘,γmercury=1.8×10−4/C∘)
A2.15 cm3B2.69 cm3C2.52 cm3D2.25 cm3 - Question 2 - Select One
A glass rod when measured with a zinc scale, both being at 30∘C, appears to be of length 100cm . If the scale shows correct reading at 0∘C, then the true length of glass rod at 30∘C and 0∘C are :-
(αglass=8×10−6^(@)C ^(-1), alpha_(z∈c)=26×10−6K−1)A100.054 cm , 100.054cmB100.078cm,100.078cmC100.078cm,100.054cmD100.054 cm , 100.078cm - Question 3 - Select One
A horizontal uniform glass tube of 100cm length is sealed at both ends contains 10cm mercury column in the middle , the temperature and pressure of air on either side of mercury column are repectively 31∘C and 76cm of mercury, if the air column at one end is kept at0∘C and the other end at 273∘C then pressure if air which is 0∘C is
(in cm of Hg)A76B88.2C102.4D122
In design of a compensated pendulum, a light metal rod of length L0 = 1.0 m is attached to a glass tube filled with mercury. Neglecting the mass of the glass tube as well, calculate the height of mercury column in the glass tube so that centre of mass of this system does not rise or fall with temperature Given : λ)Hg)=1.82×10−4K−1,αglass')=9xx10^(-6),alpha_(mηl=1.2×10−5K−1
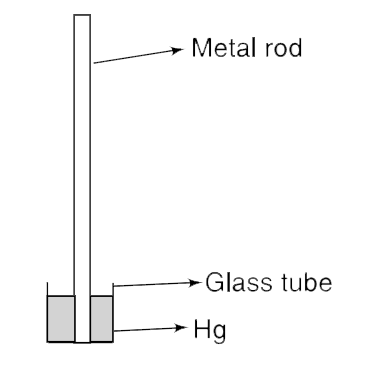 View Solution
View SolutionA mercury in glass thermometer has a stem of internal diameter 0.06 cm and contains 43 g of mercury. The mercury thread expands by 10 cm when the temperature changes from 0∘C to 50∘C. Find the coefficient of cubical expansion of mercury. Relative density of mercury =13.6 and αglass=9×10−6/K.
View SolutionA weight thermometer contains 500g of mercury at 0∘C. If the temperatue is raised to 100∘C how much mercury will be expelled. (Cubical expansivity of mercur =182×10−6.∘C−1 and that of glass =27×10−6.∘C−1)
View SolutionA porcelain crucible is filled with 1kg of mercury at room temperature (20∘C). The crucible is then placed inside a furnance, kept there for sufficient time and finally removed. It is found that it contains only 0.8Kg of mercury. Calculate the temperature of the furnace. (Average cubical expansivity of mercury =18.2×10−5K−1 and that of porcelain=2×10−5K−1)
View SolutionA two litre glass flask contains some mercury. It is found that at all temperatures the volume of the air inside the flask remains the same. The volume of the mercury inside the flask is (αfor glass =9×10−6/∘C,γ for mercury 1.8×10−4/∘C)
View Solution

