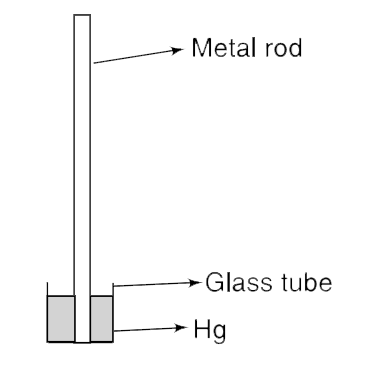
In design of a compensated pendulum, a light metal rod of length = 1.0 m is attached to a glass tube filled with mercury. Neglecting the mass of the glass tube as well, calculate the height of mercury column in the glass tube so that centre of mass of this system does not rise or fall with temperature Given :
The correct Answer is:
Topper's Solved these Questions
Similar Questions
A glass tube is attached to the bottom of a thin iron rod of length 1m. To what height must the glass tube be filled with mercury so that the centre of mass of the pendulum formed will not rise or all with changes in temperature?
(Linear expansivity of glass =9×10−6K−1, that of iron =12x10−6K−1 and cubical edxpansivity of mercury =18.2×10−5K−1)
View SolutionHeight of mercury in a barometer is h0=76.0 cm at a temperature of θ1=20∘C. If the actual atmospheric pressure does not change, but the temperature of the air, and hence the temperature of the mercury and the tube rises to θ2=35∘C, what will be the height of mercury column in the barometer now? Coefficient of volume expansion of mercury and coefficient of linear expansion of glass are
γHg=1.8×10−4.∘C−1,αg=0.09×10−4.∘C−1
View Solution
Knowledge Check
The fraction of the volume of a glass flask must be filled with mercury so that the volume of the empty space may be the same at all temperature is
(αglass=9×10−6/0C,γHg=18.9×10−5/0C)A12B17C14D15The wave length of the Green light of mercury is 550nm. If the refractive index of the glass is 1.5, the time period of the electrical vector in glass nearly (C0=3×108mS−1)
A1.8×10−9SB3.6×10−15SC9×10−15SD2.75×10−15SA glass rod when measured with a zinc scale, both being at 30∘C, appears to be of length 100cm . If the scale shows correct reading at 0∘C, then the true length of glass rod at 30∘C and 0∘C are :-
(αglass=8×10−6^(@)C ^(-1), alpha_(z∈c)=26×10−6K−1)A100.054 cm , 100.054cmB100.078cm,100.078cmC100.078cm,100.054cmD100.054 cm , 100.078cm
A glass tube of length l0 and of uniform cross-section is to be filled with mercury so that the length of the tube unoccoupied by mercury remains same at all temperatures. If γg=3α , calculate length of mercury column.
View SolutionSmall amount of mercury is poured in a glass container of 2 litres capacity. Calculate the volume of mercury in the container assuming that volume of air inside the container always remains same.
α for glass =9×10−6∘C−1
α for mercury =0.6×10−4∘C−1
View SolutionThe volume of a glass vessel is 1000 cc at 20∘C. What volume of mercury should be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are 1.8×10−4C−1 and 9.0×10−6C−1. respectively.
View SolutionThe volume of a glass vessel is 1000 cc at 20∘C. What volume of mercury could be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are 1.8×10−4∘C−1 and 9×10−6∘C−1 respectively.
View SolutionThe refractive index of glass is 1.5. Calculate the speed of light in glass. The speed of light in air is 3.0×108ms−1.
View Solution
