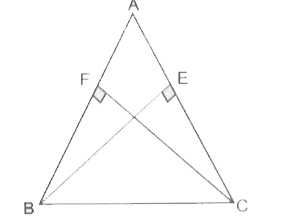
ABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that
ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.
 Solution in Kannada
Solution in Kannada
Step by step video & image solution for ABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that Delta ABE ~= Delta ACF (ii) AB = AC, i.e., ABC is an isosceles triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - SUBHASH PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Exercise 5.3
4 Videos
- TRIANGLESBOOK - SUBHASH PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Exercise 5.4
3 Videos
- TRIANGLESBOOK - SUBHASH PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Exercise 5.7
1 Video
- THREE DIMENSIONAL GEOMETRYBOOK - SUBHASH PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - TRY YOURSELF
11 Videos
- VECTOR ALGEBRA BOOK - SUBHASH PUBLICATIONCHAPTER - VECTOR ALGEBRA EXERCISE - TRY YOURSELF
4 Videos
Similar Questions
AD is an altiude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC (ii) AD bisects A.
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
View SolutionConstruct a triangle PQR in which QR = 6 cm, Q=60∘ and PR = PQ = 2cm.
View SolutionFind the equation of the plane through the intersection of the planes 3x−y+2z−4=0 and z+y+z−2=0 and the point (2,2,1).
View SolutionFind the area of the triangle with vertices A(1,1,2), B(2,3,5) and C(1,5,5).
View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलम्ब BE और CF बराबर है। दर्शाइए कि
(i) ΔABE≅ΔACF
(ii) AB=AC, अर्थात ΔABC एक समद्विबाहु त्रिभुज है।
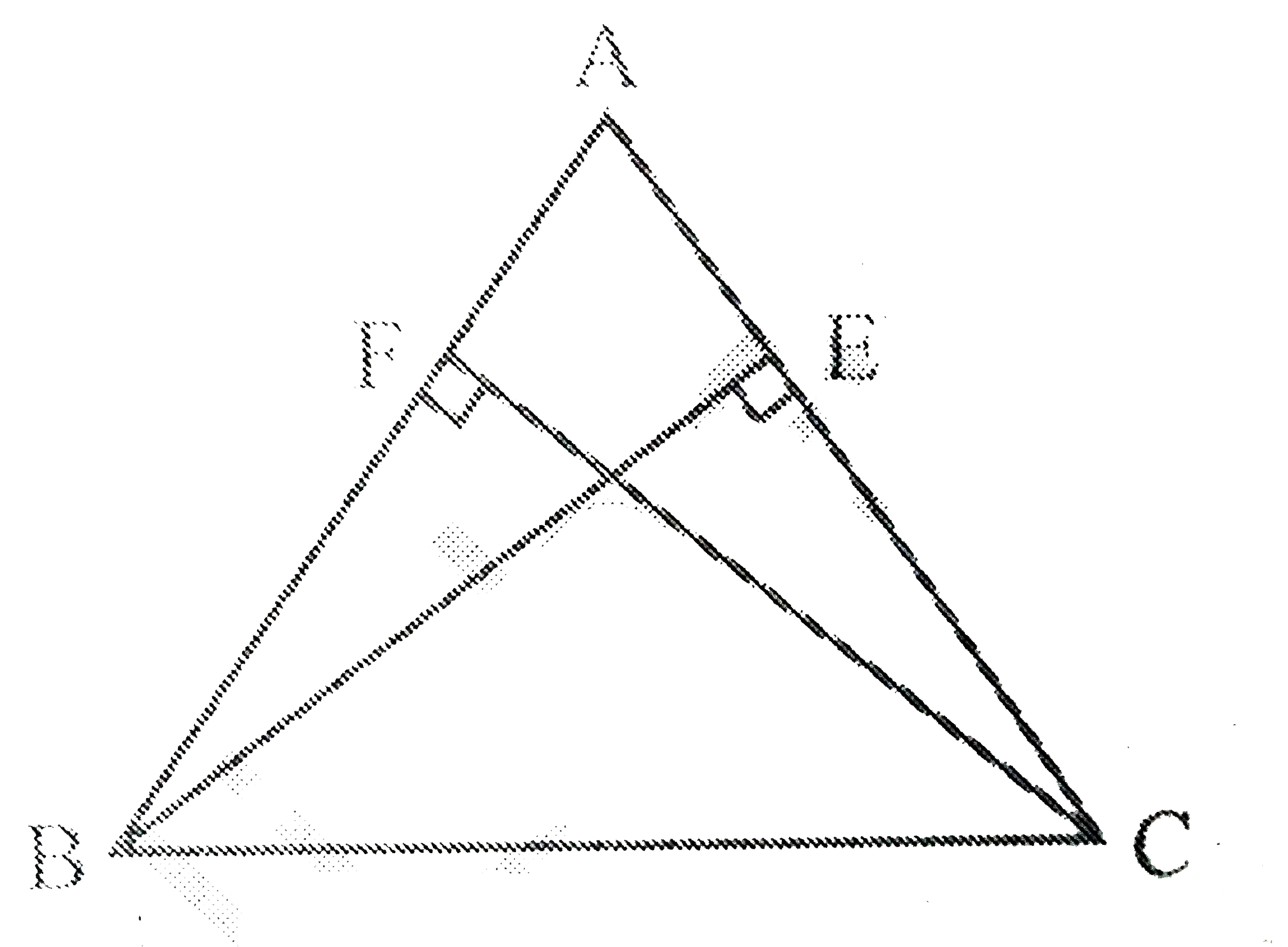
View Solutionएक त्रिभुज ABC है जिसमें ऊँचाइयाँ BE और CF भुजाओं AC और AB के बराबर है तो दिखाइये कि-
(i) ΔABE≅ΔACF
(ii) AB=AC,अर्थात ABC एक समद्विबाहु त्रिभुज है ।

View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.

View SolutionABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.
View SolutionΔABC లో AC,AB భుజాలకు గీసిన లంబాలు BE,CF లు సమానము అయిన AB =AC అనగా ΔABC ఒక సమద్విబహు త్రిభుజామని చూపండి.

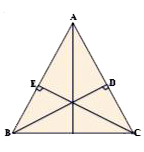
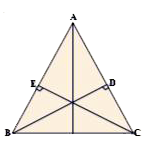
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
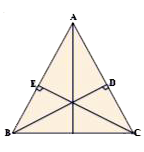
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
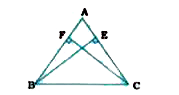
View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see the given figure). Show that ( i ) △ABE≅△ACF
(ii) AB = AC i.e ABC is an isoceles triangle
View Solution
