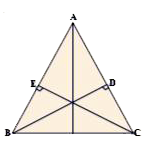
ABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
 Solution in Kannada
Solution in Kannada
Step by step video & image solution for ABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that (i) DeltaABD ~= DeltaACE (ii) AB = AC i.e., ABC is an isosceles triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - NCERT KANNADCHAPTER - TRIANGLES EXERCISE - EXERCISE - 7.3
7 Videos
- TRIANGLES BOOK - NCERT KANNADCHAPTER - TRIANGLES EXERCISE - EXERCISE - 7.4
7 Videos
- TRIANGLES BOOK - NCERT KANNADCHAPTER - TRIANGLES EXERCISE - EXERCISE - 7.1
11 Videos
- THE ELEMENTS OF GEOMETRY BOOK - NCERT KANNADCHAPTER - THE ELEMENTS OF GEOMETRY EXERCISE - BRAIN TEASER
2 Videos
Similar Questions
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
View SolutionShow that in a right angled triangle, the hypotenuse is the longest side.
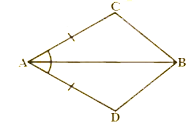
View SolutionIn quadrilateral ACBD,AC=ADandAB bisects ∠A Show that ΔABC≅ΔABD.
What can you say about BC and BD?
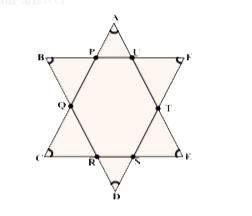
View SolutionWhat is the measure of ∠A+∠B+∠C+∠D+∠E+∠F in the figure given below. Give reason to your answer.
View SolutionIn the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.

View SolutionIn the following figure, AB and BC are equidistant from the centre 'O' of the Show that
(a) ABC is an isosceles triangle.
(b) OB bisects angle ABC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_X_C13_E02_006_Q01.png" width="80%"gt
View SolutionIn the following figure (not to scale), ABC is a right isosceles triangle, right- angle at B and BD⊥AC. If the triangle ABC is rotated about the hypotenuse, then find the locus of the triangle ABC. ltbr gt ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E02_006_Q01.png" width="80%"gt
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View SolutionABC is a triangle in which altitude BE and CF to sides AC and AB are equal. Show that
ΔABE≅ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.

View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
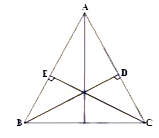
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
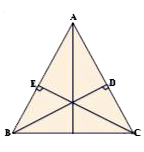
View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
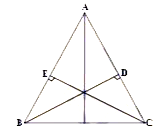
View SolutionABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure) . Show that
(i)ΔABD≅ΔACE
(ii)AB=AC i.e., ABC is an isosceles triangle.
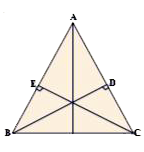
View SolutionABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure) Show that these altitudes are equal.
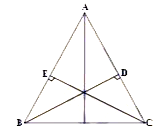
View SolutionABC एक त्रिभुज है जिसमे AC और AB पर खिचे गए शीर्षलम्ब BE और CF बराबर है ( देखिए आक्रति ) | दर्शाइए कि- (i) ΔABE ~-= ΔACF
(ii) AB -= AC, अर्थात ΔABC एक समद्धिबाहू त्रिभुज है |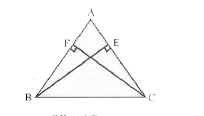
View Solution
