The points P,Q,R and S lie in that order on a straight line . The midpoint of ¯¯¯¯¯¯QS is R and the midpoint of ¯¯¯¯¯PS is Q . The length of ¯¯¯¯¯¯QR is x feet and the length of ¯¯¯¯¯¯PQ is 4x−16 feet . What is the length , in feet , of ¯¯¯¯¯PS?
32
20
16
8
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the relationships between the points
We know that:
- Points P, Q, R, and S lie on a straight line in that order.
- R is the midpoint of segment QS.
- Q is the midpoint of segment PS.
- The length of segment QR is x feet.
- The length of segment PQ is 4x−16 feet.
Step 2: Establish the lengths of segments based on midpoints
Since R is the midpoint of QS, we have:
- QR=x
- RS=x
Thus, the total length of segment QS is:
QS=QR+RS=x+x=2x
Since Q is the midpoint of PS, we have:
- PQ=4x−16
And since Q is the midpoint of PS:
PQ=QS
This gives us the equation:
4x−16=2x
Step 3: Solve the equation for x
Now, we will solve the equation:
4x−16=2x
Subtract 2x from both sides:
4x−2x−16=0
2x−16=0
Add 16 to both sides:
2x=16
Now, divide by 2:
x=8
Step 4: Find the length of segment PS
Now that we have x, we can find the length of PS. The length of PS can be calculated as:
PS=PQ+QR+RS
Substituting the known lengths:
- PQ=4x−16
- QR=x
- RS=x
So,
PS=(4x−16)+x+x
PS=4x−16+2x
PS=6x−16
Now substitute x=8:
PS=6(8)−16
PS=48−16
PS=32
Final Answer
The length of segment PS is 32 feet.
---
We know that:
- Points P, Q, R, and S lie on a straight line in that order.
- R is the midpoint of segment QS.
- Q is the midpoint of segment PS.
- The length of segment QR is x feet.
- The length of segment PQ is 4x−16 feet.
Since R is the midpoint of QS, we have:
- QR=x
- RS=x
QS=QR+RS=x+x=2x
- PQ=4x−16
PQ=QS
This gives us the equation:
4x−16=2x
Now, we will solve the equation:
4x−16=2x
4x−2x−16=0
2x−16=0
2x=16
x=8
Now that we have x, we can find the length of PS. The length of PS can be calculated as:
PS=PQ+QR+RS
- PQ=4x−16
- QR=x
- RS=x
PS=(4x−16)+x+x
PS=4x−16+2x
PS=6x−16
PS=6(8)−16
PS=48−16
PS=32
The length of segment PS is 32 feet.
Topper's Solved these Questions
Similar Questions
n=12×2t3
The number of mice in a certain colony is shown by the formula above, such that n is the number of mice and t is the time, in months, since the start of the colony. IF 2 years have passed since the start of the colony, how many mice does the colony contain now?
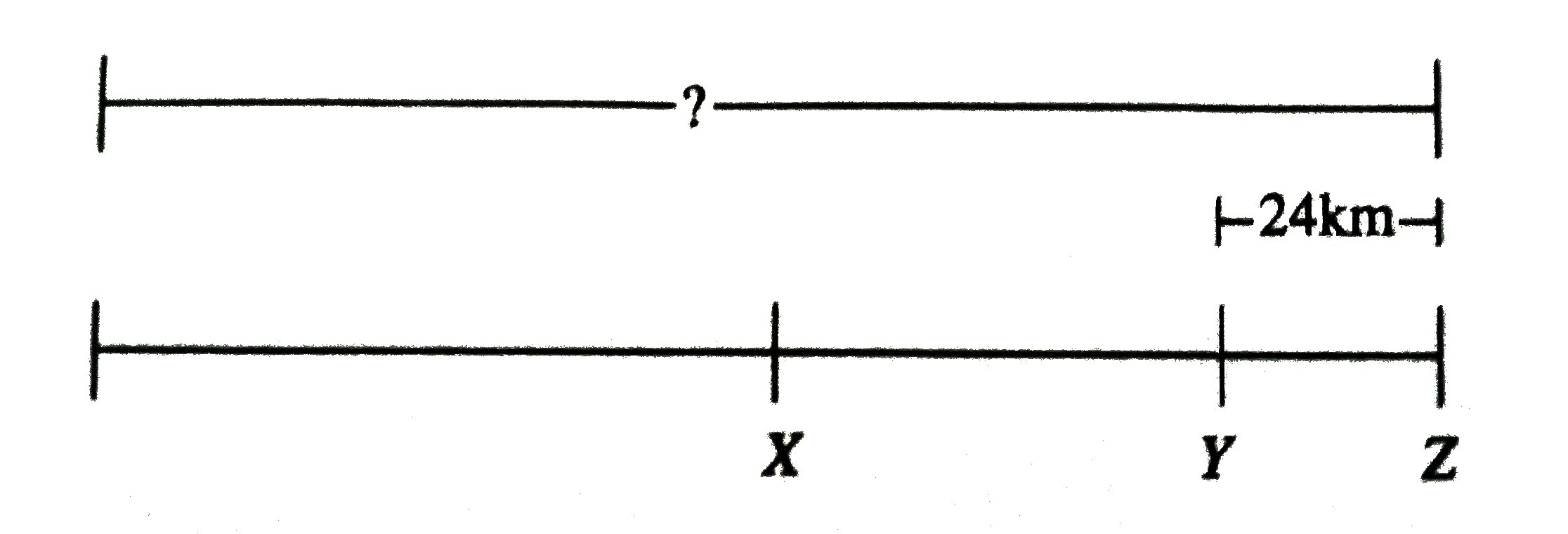
View SolutionIn the hiking trail shown below .X marks the trail's halfway point .If ¯¯¯¯¯¯YZ measures 24 kilometers and is 13 the length of ¯¯¯¯xz , what is the total length , in kilometers of the trail ?
View SolutionP,Q,R,S have position vectors bar(p),bar(q),bar(r),bar(s) respctively such that (bar(p)-bar(q))=2(bar(s)-bar(r)) then QS and PR
View SolutionIf bar(p)bar(q)bar(r) is reciprocal system of vector triad bar(a),bar(b) and bar(c) then [bar(a)bar(b)bar(c)][bar(p)bar(q)bar(r)]=
View SolutionIf bar(a),bar(b),bar(c) and bar(p),bar(q)bar(r) are two sets of three non- coplanar vectors such that bar(a)*bar(p)+bar(b).bar(q)+bar(c).bar(r)=3 then bar(P)=.......bar(q)=......,bar(r)=......
View SolutionIf bar(p) and bar(s) are not perpendicular to each other and bar(r)xxbar(p)=bar(q)xxbar(p)o*bar(r).bar(s)=0, then bar(r) is
View SolutionDraw a line segment AB = 7.6 cm. without constructing parallel lines at A and B, find three points P,Q and R on bar(AB) such that bar(AP)=bar(PQ)=bar(QR)=bar(RB).
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
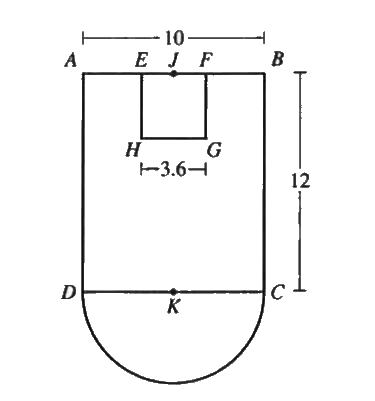
What is the length, in meters, of ¯¯¯¯¯¯JD?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
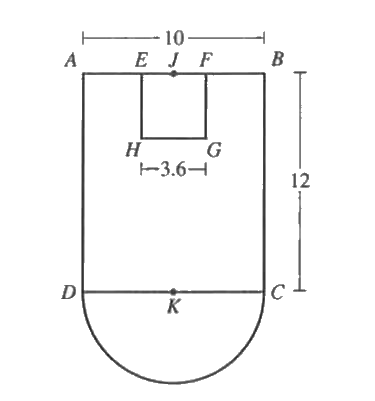
What is the length, in meters, of are ¯¯¯¯¯¯CD?
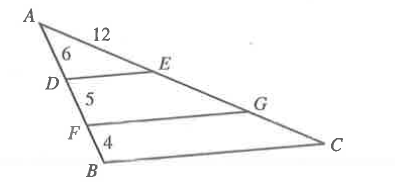
View SolutionIn the figure shown below, E and G lie on ¯¯¯¯¯¯AC, D and F lie on ¯¯¯¯¯¯AB,¯¯¯¯¯¯DEand¯¯¯¯¯¯FG are parallel to ¯¯¯¯¯¯BC, and the given lengths are in feet. What is the length of ¯¯¯¯¯¯AC, in feet?
View SolutionThree vectors ¯¯¯P,¯¯¯Qand¯¯¯R are shown in the figure.Let S be any point on the vector bar(R) .The distance between the points P and S is b|bar(R)| .The general relation among vectors bar(P) bar(Q) and bar(S) is qquad Y
View SolutionThree vectors bar(P) bar(Q) and bar(R) are shown in the figure.Let S be any point on the vector bar(R) .The distance between the points P and S is b|bar(R)| .The general relation among vectors bar(P) bar(Q) and bar(s) is
View SolutionP = (-5, 4) and Q = (-2, -3). If ¯¯¯¯¯¯PQ is produced to R such that P divides ¯¯¯¯¯¯QR externally in the ratio 1:2, then R is
View Solutionयदि ABCD कोई चतुर्भुज हो तो सिद्ध कीजिए कि
¯¯¯¯¯¯AB+¯¯¯¯¯¯AD+¯¯¯¯¯¯CB¯¯¯¯¯¯CD=4¯¯¯¯¯¯PQ
जहां P और Q क्रमशः AC और BD के मध्य बिंदु हैं।
View SolutionPoint A, B, and C all lie on a line. Point D is midpoint of ¯¯¯¯¯¯AB and E is the midpoint of BC,¯¯¯¯¯¯AB=4and¯¯¯¯¯¯BC=10. Which of the following could be the length of ¯¯¯¯¯¯AE?
View Solution
