For all t>0,f(x)=t2−1t−1−t . Which of the following is true about f(t) ?
It increases in proportion to t.
It increases in proportion to t2.
It decreases in proportion to t.
It remains constant .
The correct Answer is:D
To solve the problem, we need to analyze the function given and determine its behavior as t varies. The function is defined as:
f(t)=t2−1t−1−t
Step 1: Simplify the function
We start by simplifying f(t).
The numerator t2−1 can be factored using the difference of squares:
t2−1=(t−1)(t+1)
Thus, we can rewrite f(t):
f(t)=(t−1)(t+1)t−1−t
Step 2: Cancel common terms
Since t>0 and t≠1, we can cancel t−1 in the numerator and denominator:
f(t)=t+1−t
Step 3: Simplify further
Now, we simplify the expression:
f(t)=1
Step 4: Analyze the result
The function f(t) simplifies to a constant value of 1, regardless of the value of t (as long as t>0).
Conclusion
Since f(t)=1 is constant, we can conclude that:
- f(t) does not increase or decrease with respect to t.
- Therefore, the correct option is that it remains constant.
Final Answer
The correct statement about f(t) is that it remains constant.
---
We start by simplifying f(t).
Since t>0 and t≠1, we can cancel t−1 in the numerator and denominator:
Now, we simplify the expression:
The function f(t) simplifies to a constant value of 1, regardless of the value of t (as long as t>0).
Since f(t)=1 is constant, we can conclude that:
- Therefore, the correct option is that it remains constant.
The correct statement about f(t) is that it remains constant.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If f(x)=t2+32t, then f(q−1)=
Aq2−32Bq2−12qCq2+12q+12Dq2−12q−12 - Question 2 - Select One
For any arbitrary motion in space, which of the following relations are true?
a) vaverage=(1/2)(v(t1+v(t2)
b) vaverage=[r(t2)−rt1t2−t1
v(t)=v(0)+at
d) aaverage=[v(t2)−vt1t2−t1
The average stands for average of the quantity over time interval t1 to t_(2)A→vaverage=12[→v(t1)+→v(t2)]B→vaverage=→r(t2)−→r(t1)t2−t1C→v(t)=→v(0)+→atD→r(t)=→r(0)+→v(0)t+12→at2
Let f(x)=(1−x)2sin2x+x2 for all x∈IR and let g(x)=∫x1(2(t−1)t+1−lnt)f(t) dt for all x∈(1,∞).
Which of the following is true ?View SolutionShown below are the black body radiation curves at temperature T1 and T2(T2>T1). Which of the following plots is correct?
View Solution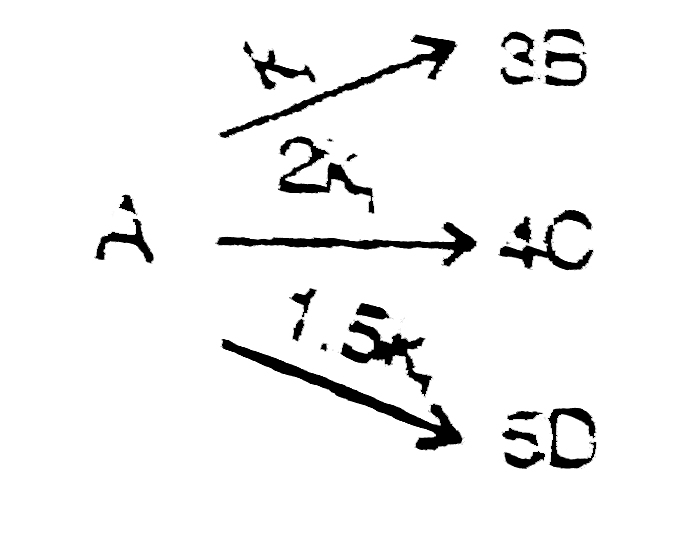
All reactions are of 1st order .
At time t=t1(t1>0)
[B][C]=αTherefore at
time t=t2 (where t2≥t1)
[C][D]=βWhich of the following is correct ?View SolutionLet f(x)=(1−x)2sin2x+x2 for all x ∈ R, and let g(x)=∫(2(t−1)t+1−lnt)f(t)dt for t ∈ [1, x] for all x ∈ (1, ∞).Which of the following is true ?
View SolutionLet f(x)=∫x0(t−1)(t−2)2dt, then find a point of minimum.
View Solutionf(x)=∫x0et3(t2−1)(t+1)2011dt(x>0) then :
View Solution

