Which of the following can represent the curve x2=−2y ?
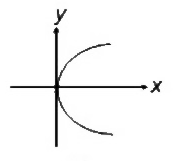
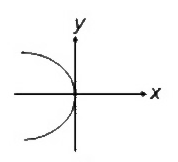
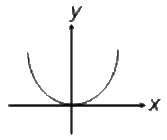
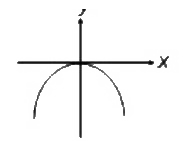
The correct Answer is:D
To solve the equation x2=−2y and determine its representation, we can follow these steps:
Step 1: Rearranging the Equation
Start by rearranging the equation to express y in terms of x:
x2=−2y⟹y=−12x2
Step 2: Understanding the Form of the Equation
The equation y=−12x2 is a quadratic equation in x. It represents a parabola that opens downwards because the coefficient of x2 is negative.
Step 3: Identifying the Vertex
The vertex of the parabola can be found from the equation y=−12x2. The vertex occurs at the point where x=0:
y=−12(0)2=0
Thus, the vertex is at the point (0,0).
Step 4: Analyzing the Symmetry
The parabola is symmetric about the y-axis because the equation involves x2. This means that for every positive x, there is a corresponding negative x that gives the same y value.
Step 5: Sketching the Graph
To sketch the graph, we can plot a few points:
- For x=1, y=−12(1)2=−12 → Point (1, -0.5)
- For x=−1, y=−12(−1)2=−12 → Point (-1, -0.5)
- For x=2, y=−12(2)2=−2 → Point (2, -2)
- For x=−2, y=−12(−2)2=−2 → Point (-2, -2)
Plotting these points will show that the parabola opens downwards and is symmetric about the y-axis.
Step 6: Conclusion
The curve represented by the equation x2=−2y is a downward-opening parabola with its vertex at the origin (0, 0).
Start by rearranging the equation to express y in terms of x:
x2=−2y⟹y=−12x2
The equation y=−12x2 is a quadratic equation in x. It represents a parabola that opens downwards because the coefficient of x2 is negative.
The vertex of the parabola can be found from the equation y=−12x2. The vertex occurs at the point where x=0:
y=−12(0)2=0
Thus, the vertex is at the point (0,0).
The parabola is symmetric about the y-axis because the equation involves x2. This means that for every positive x, there is a corresponding negative x that gives the same y value.
To sketch the graph, we can plot a few points:
- For x=1, y=−12(1)2=−12 → Point (1, -0.5)
- For x=−1, y=−12(−1)2=−12 → Point (-1, -0.5)
- For x=2, y=−12(2)2=−2 → Point (2, -2)
- For x=−2, y=−12(−2)2=−2 → Point (-2, -2)
The curve represented by the equation x2=−2y is a downward-opening parabola with its vertex at the origin (0, 0).
Similar Questions
Which of the following are true for the curve represented by the differential equation sec2ydydx+2xtany=x3 satisfying y(1)=0 (A) equation of curve is 2tany=x2−1 (B) equation of curve is y2=x3−1 (C) curve is a parabola (D) curve is not a conic
View SolutionThe differential equation of the family of curves represented by the equation x2y=a. is
View Solution
Knowledge Check
- Question 1 - Select One
Which of the following may represent the curve x = 2y+ 3?
A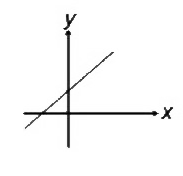 B
B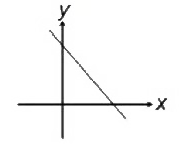 C
C D
D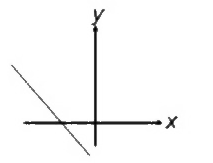
- Question 2 - Select One
Let y=f(x)={e1x2ifx≠00ifx=0 then which of the following can best represent the graph of y=f(x)?
A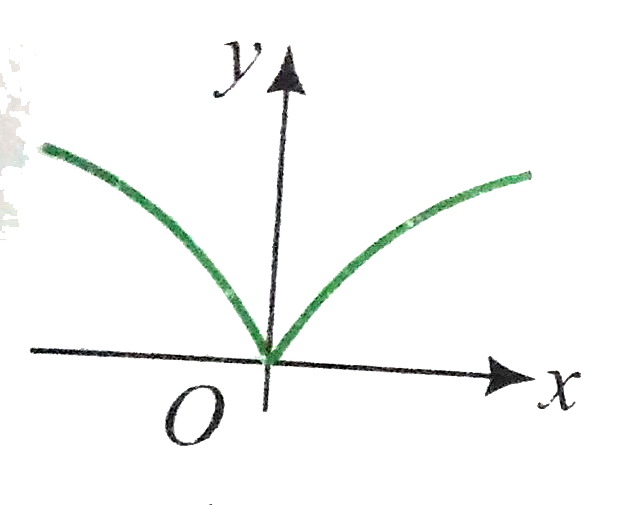 B
B C
C D
D
- Question 3 - Select One
Which of the following is represented by 'Lorenz Curve'?
AEmploymentBInflationCDeflationDIncome distribution
Which of the following options is not the asymptote of the curve 3x3+2x2y−7xy2+2y3−14xy+7y2+4x+5y=0?
View SolutionWhich one of the following curves cut the parabola at right angles? x2+y2=a2 (b) y=e−x/2a y=ax (d) x2=4ay
View SolutionConsider curve y=(1+x)y+sin−1(sin2x). Which of the following statements are correct ?
View SolutionWhich of the following curves represents a zero order reaction ? [(a−x) =reactant concn.]
View SolutionThe eccentricity of the curve represented by the equation x2+2y2−2x+3y+2=0 is
View Solution

