Show here are the velocity and acceleration vectors for an object in several different types of motion. In which case is the object slowing down and turning to the left ?
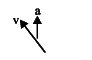
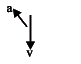
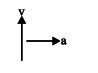
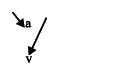
The correct Answer is:B
To determine in which case the object is slowing down and turning to the left, we need to analyze the relationship between the velocity and acceleration vectors in each scenario. Here’s a step-by-step solution:
Step 1: Understand the Concept of Deceleration
- Deceleration (or retardation) occurs when the acceleration vector is opposite to the velocity vector. This means that the object is slowing down.
Step 2: Analyze the Direction of Turning
- For an object to turn to the left, there must be a component of the acceleration vector that points to the left of the velocity vector. This component will cause the object to change its direction towards the left.
Step 3: Examine Each Case
1. First Case:
- The acceleration vector has a component that is parallel to the velocity vector (in the same direction), which means the object is speeding up. The perpendicular component is directed to the right, causing a right turn.
- Conclusion: This case does not satisfy our conditions.
2. Second Case:
- The acceleration vector has a component that is opposite to the velocity vector (deceleration), which means the object is slowing down. Additionally, there is a component of acceleration directed to the left of the velocity vector, causing the object to turn left.
- Conclusion: This case satisfies both conditions of slowing down and turning left.
3. Third Case:
- The acceleration vector is perpendicular to the velocity vector, meaning there is no component acting in the direction of the velocity. The object maintains a uniform motion and does not slow down or speed up.
- Conclusion: This case does not satisfy our conditions.
4. Fourth Case:
- The acceleration vector has a component along the velocity vector (speeding up) and a perpendicular component that may cause a left turn. However, since the object is speeding up, it does not meet the slowing down condition.
- Conclusion: This case does not satisfy our conditions.
Final Conclusion
- The second case is the only scenario where the object is slowing down and turning to the left.
- Deceleration (or retardation) occurs when the acceleration vector is opposite to the velocity vector. This means that the object is slowing down.
- For an object to turn to the left, there must be a component of the acceleration vector that points to the left of the velocity vector. This component will cause the object to change its direction towards the left.
1. First Case:
- The acceleration vector has a component that is parallel to the velocity vector (in the same direction), which means the object is speeding up. The perpendicular component is directed to the right, causing a right turn.
- Conclusion: This case does not satisfy our conditions.
- The acceleration vector has a component that is opposite to the velocity vector (deceleration), which means the object is slowing down. Additionally, there is a component of acceleration directed to the left of the velocity vector, causing the object to turn left.
- Conclusion: This case satisfies both conditions of slowing down and turning left.
- The acceleration vector is perpendicular to the velocity vector, meaning there is no component acting in the direction of the velocity. The object maintains a uniform motion and does not slow down or speed up.
- Conclusion: This case does not satisfy our conditions.
- The acceleration vector has a component along the velocity vector (speeding up) and a perpendicular component that may cause a left turn. However, since the object is speeding up, it does not meet the slowing down condition.
- Conclusion: This case does not satisfy our conditions.
- The second case is the only scenario where the object is slowing down and turning to the left.
Similar Questions
Name the different types of celestial objects which are members of the Solar System.
View SolutionMatch the following.
At a certain moment in time the angle between the velocity →v of a particle and the acceleration vector a of that particle is 0. Match the type of motion of the particle at this moment for different θ is
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows the velocity-displacement curve for an object moving along a straight line. At which of the points marked is the object speeding up?
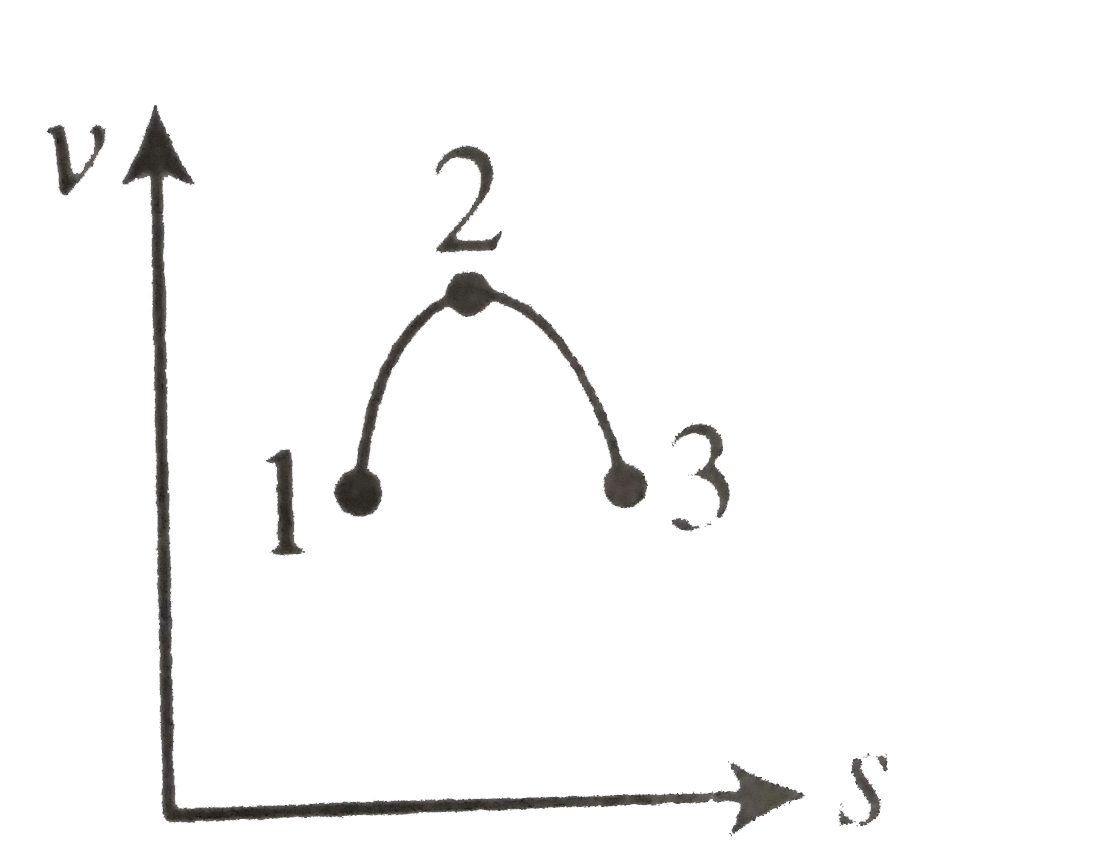A1B2C1 and 3D1,2, and 3 - Question 2 - Select One
Figure shows path followed by a particle and position of a particle at any instant. Four different students have represented the velocity vectors and acceleration vectors at the given instant. Which vector diagram can not be true in any situation? (In each figure velocity is tangential to the trajectory).
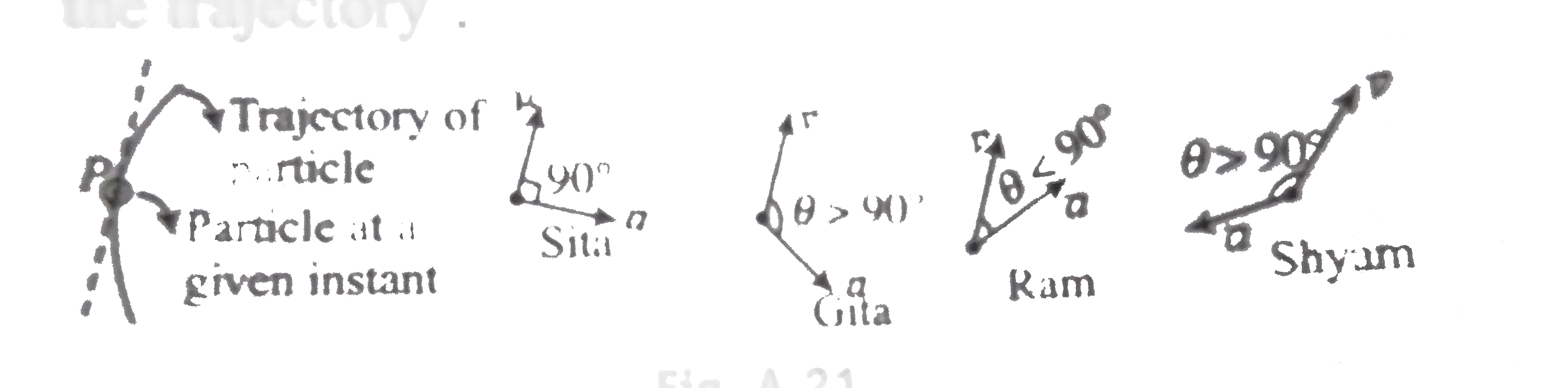ASitaBGitaCRamDShyam - Question 3 - Select One
Figure shows a path followed by a particle and position of a particle at any instant. Four different students have represented the velocity vectors and acceleration vectors at the given instant. Which vector diagram cannot be true in any situation? (In each figure, velocity is tangential to the trajectory).
A15ms−1B30ms−1C10ms−1D25ms−1
The relation between the acceleration and time for an object is given below. Calculate the velocity with which the object is moving at t = 1 s.
a=3t−4t2View SolutionSay Yes or No:
a. Can an object moving towards north have acceleration towards south?
b. Can an object reverse the direction of its motion even thouth it has reverse the direcleration?
C. Can an object reverse the derction of its acceleration even though it continues to move in the same dirction?
d. Average speed is the magnitude of average velocity
e. At any instant of time. the directions of change in velocity and acceleration are differnt.View SolutionVibration indicates which type of motion of an object
View SolutionFigure shows the velocity and acceleration of a point line body at the initial moment of its motion. The acceleration vector of the body remains constant. The minimum radius of curvature of trajectory of the body is
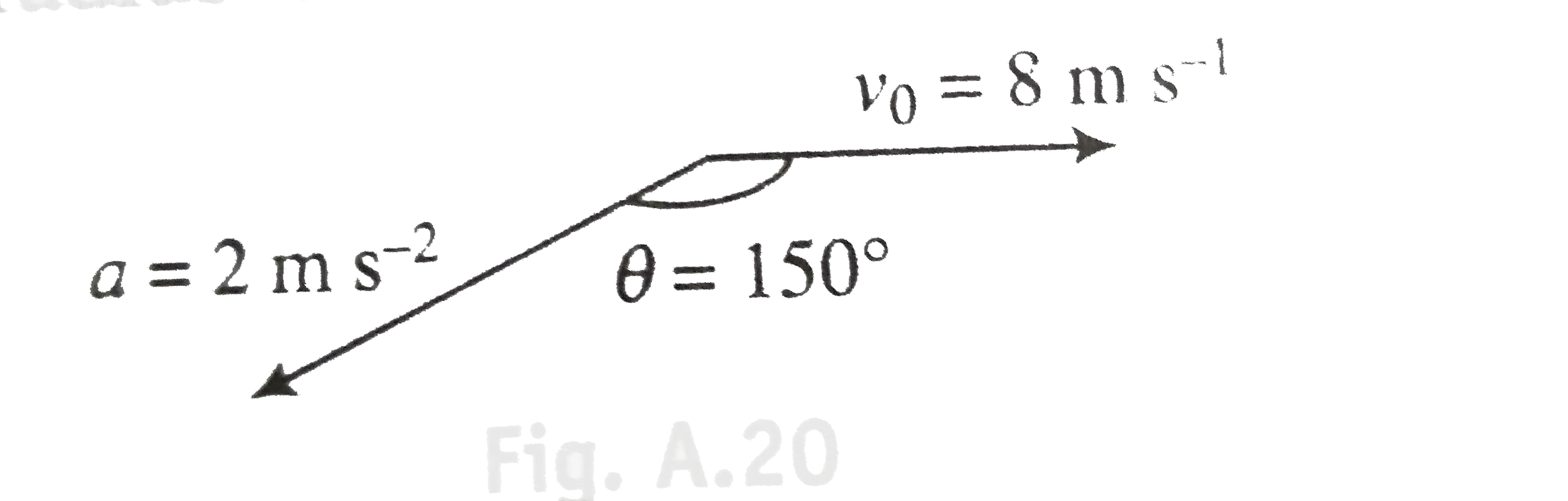View SolutionEach of the three graphs represents acceleration versus time for an object that already has a positive velocity at time t1. Which graphs show an object whose speed is increasing for the entire time interval between t1 and t2?
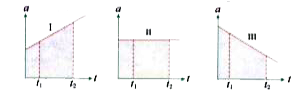View Solution