Given that C denotes capacitance of a capacitor and V is the potential difference across its plates. Then the dimensions of CV2 are same as that of
momentum
power
forces
torque
The correct Answer is:D
To find the dimensions of CV2, where C is the capacitance and V is the potential difference, we can follow these steps:
1. Identify the dimensions of capacitance C:
The capacitance C is defined as the charge Q per unit potential difference V. The formula is:
C=QV
The dimension of charge Q is (I)(T) (where I is current and T is time). The dimension of potential difference V is (M)(L2)(T−3)(I−1) (derived from the formula V=W/Q, where W is work done, and its dimension is (M)(L2)(T−2)).
Therefore, the dimension of capacitance C can be expressed as:
(C)=(Q)(V)=(I)(T)(M)(L2)(T−3)(I−1)=(M−1)(L−2)(T4)(I2)
2. Identify the dimensions of potential difference V:
As mentioned earlier, the dimension of potential difference V is:
(V)=(M)(L2)(T−3)(I−1)
3. Calculate the dimensions of V2:
To find V2, we square the dimensions of V:
(V2)=((M)(L2)(T−3)(I−1))2=(M2)(L4)(T−6)(I−2)
4. Combine the dimensions of C and V2:
Now we can find the dimensions of CV2:
(CV2)=(C)⋅(V2)=(M−1)(L−2)(T4)(I2)⋅(M2)(L4)(T−6)(I−2)
5. Multiply the dimensions:
When we multiply the dimensions, we combine the powers of each base unit:
(CV2)=(M−1⋅M2)(L−2⋅L4)(T4⋅T−6)(I2⋅I−2)
This simplifies to:
(CV2)=(M1)(L2)(T−2)(I0)=(M)(L2)(T−2)
6. Conclusion:
The dimensions of CV2 are the same as that of energy, which is given by:
(E)=(M)(L2)(T−2)
Final Answer:
The dimensions of CV2 are the same as that of energy.
The capacitance C is defined as the charge Q per unit potential difference V. The formula is:
C=QV
The dimension of charge Q is (I)(T) (where I is current and T is time). The dimension of potential difference V is (M)(L2)(T−3)(I−1) (derived from the formula V=W/Q, where W is work done, and its dimension is (M)(L2)(T−2)).
(C)=(Q)(V)=(I)(T)(M)(L2)(T−3)(I−1)=(M−1)(L−2)(T4)(I2)
As mentioned earlier, the dimension of potential difference V is:
(V)=(M)(L2)(T−3)(I−1)
To find V2, we square the dimensions of V:
(V2)=((M)(L2)(T−3)(I−1))2=(M2)(L4)(T−6)(I−2)
Now we can find the dimensions of CV2:
(CV2)=(C)⋅(V2)=(M−1)(L−2)(T4)(I2)⋅(M2)(L4)(T−6)(I−2)
When we multiply the dimensions, we combine the powers of each base unit:
(CV2)=(M−1⋅M2)(L−2⋅L4)(T4⋅T−6)(I2⋅I−2)
This simplifies to:
(CV2)=(M1)(L2)(T−2)(I0)=(M)(L2)(T−2)
The dimensions of CV2 are the same as that of energy, which is given by:
(E)=(M)(L2)(T−2)
The dimensions of CV2 are the same as that of energy.
Similar Questions
Knowledge Check
- Question 1 - Select One
The displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
Abecomes zeroBhas assumed a constant valueCis increasing with timeDdecreasing with time - Question 2 - Select One
If V denotes te potential difference across the plate of a capacitor of capacitance C, the dimensions of CV2 are
ANot expressible in MLTBMLT−2CM2LT−1DML2T−2 - Question 3 - Select One
If L,R,C,andV, respectively , represent inductance , resistance , capacitance and potential difference , then the dimensions of L/RCV are the same as those of
AChargeB1/ChargeCCurrentD1/Current
The charge stored in a capacitor is 20μ C and the potential difference across the plates is 500V .Its capacity is ..?
View SolutionIf C be the capacitance and V be the electric potential, then the dimensional formula of CV2 is
View SolutionIf C be the capacitance and V be the electric potential, then the dimensional formula of CV2 is
View SolutionIn the circuit diagram given below, the value of the potential difference across the plates of the capacitors are.
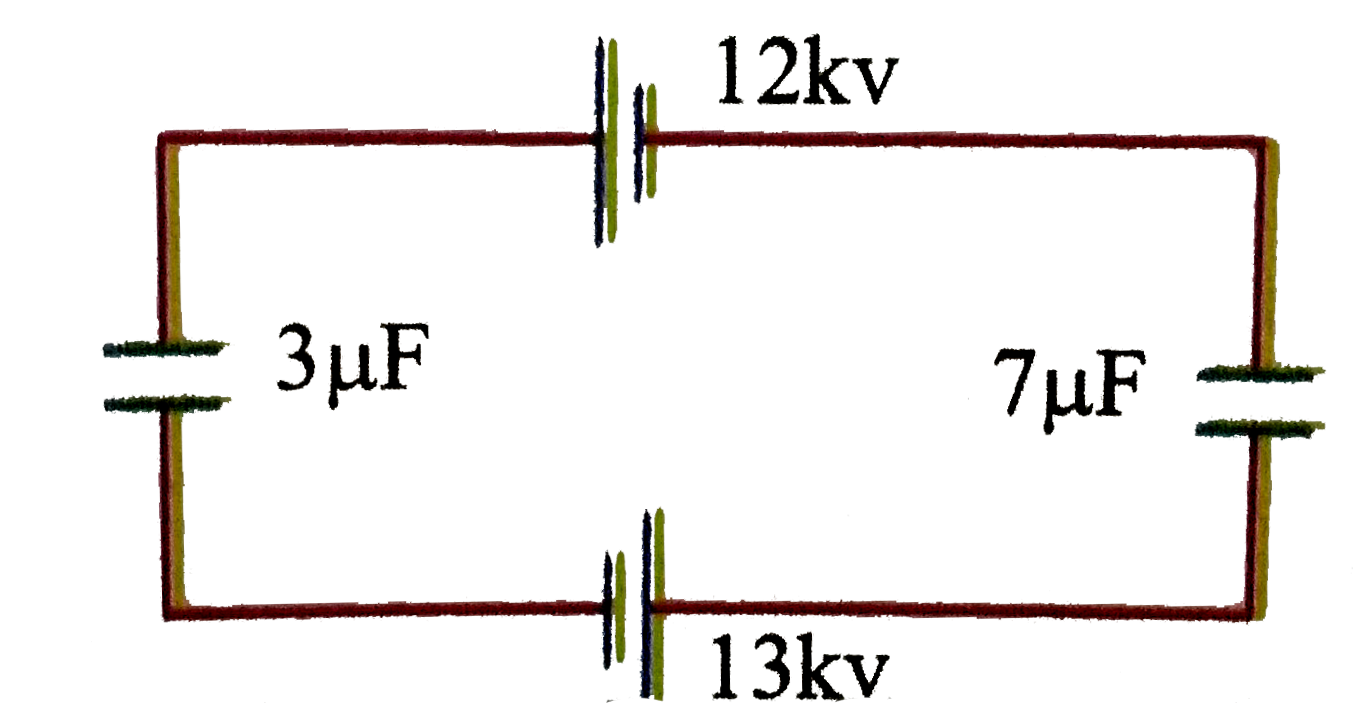 .View Solution
.View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View Solution