A block of mass m is placed on a wedge of mass M. Coefficient between then is μ<cotθ. The wedge is given an acceleration to its left. Find the maximum acceleration at which block apears stationary relative to wedge.

g(sinθ−μcosθ)cosθ+μsinθ
g(sinθ+μcosθ)cosθ−μsinθ
g(cosθ+μsinθ)cosθ−μcosθ
g(cosθ−μsinθ)cosθ+μcosθ
The correct Answer is:2
Step by step video & image solution for A block of mass m is placed on a wedge of mass M. Coefficient between then is mu lt cot theta . The wedge is given an acceleration to its left. Find the maximum acceleration at which block apears stationary relative to wedge. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Figure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
View SolutionA block of mass m is placed on a smooth wedge of inclination θ. The while system is acceleration horizontally so that the block does not slip. Find (a) horizontal acceleration, (b) normal force between the block and the wedge and (c) the horizontal force applied on the wedge.
View Solution
Knowledge Check
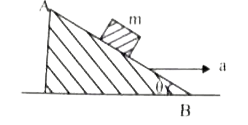
A block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθA block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθA block of mass m resting on a wedge of angle θ as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m falls freely ?
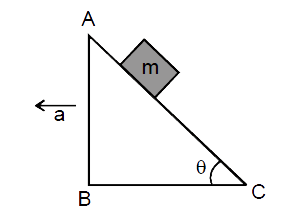 AgBgcosθCgcotθDgtanθ
AgBgcosθCgcotθDgtanθ
A block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View SolutionA block of mass m is placed on a smooth wedge of inclination. The whole system is accelerated horizontally so that block does not slip on the wedge Find the i) Acceleration of the wedge Force to be applied on the wedge Force exerted by the wedge on the block .
View Solutiona Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
View SolutionA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
View Solution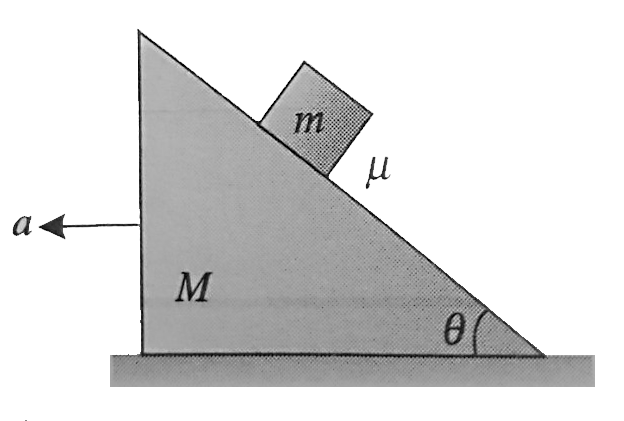
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View Solution
