A block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.

a=gtanθ
a=gcosecθ
a=cosθ
a=gsinθ
The correct Answer is:A
If the block is stationary, macosθ=mgsinθ
which gives a=>anθ . 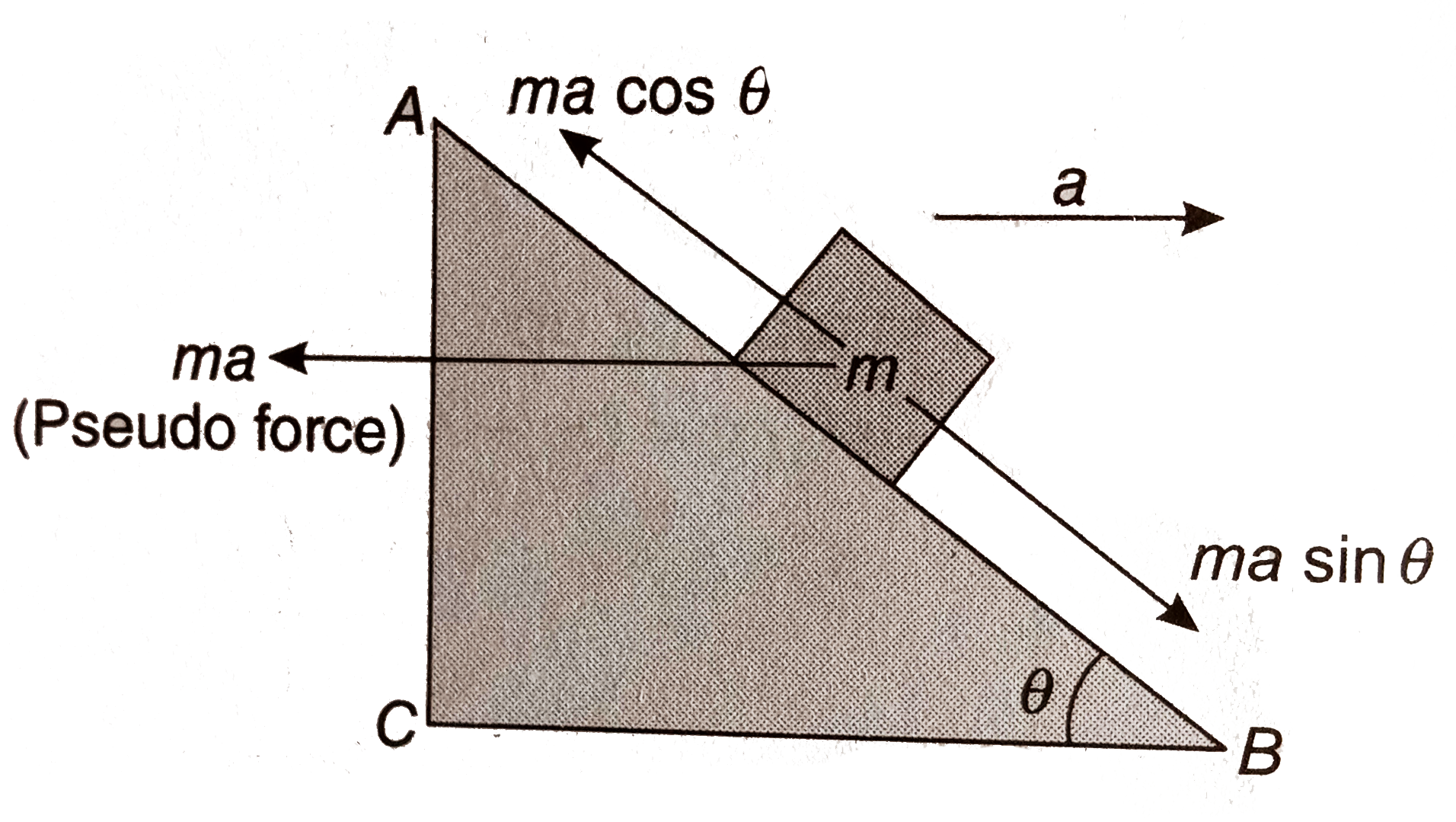
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - AIIMS Questions
26 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Assertion Reasoning
14 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
Similar Questions
A block of mass m is placed on the rough incline of a wedge of mass M and inclination α to the horizontal. Calculate the maximum and minimum acceleration that can be imparted to the wedge so that the block may remain stationary relative to the wedge. The coefficient iof friction between the block and the wedge is μ.
View SolutionA block of mass m is placed on a wedge of mass M. Coefficient between then is μ<cotθ. The wedge is given an acceleration to its left. Find the maximum acceleration at which block apears stationary relative to wedge.

View Solution
Knowledge Check
A block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθA block of mass m resting on a wedge of angle θ as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m falls freely ?
 AgBgcosθCgcotθDgtanθ
AgBgcosθCgcotθDgtanθA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
A(M+m)gB(M+msinθ)gCMgD(M+msinθM+m)gcosθ
Figure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
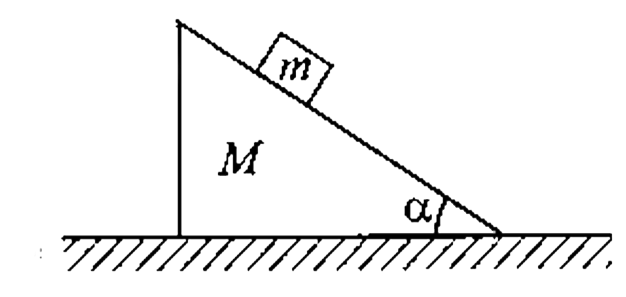
View SolutionA smooth block of mass m is held stationary on a smooth wedge of mass M and inclination θ as shown in figure .If the system is released from rest , then the normal reaction between the block and the wedge is

View SolutionA block of mass m is placed on a smooth wedge of incination θ. The whole system s acelerated horizontally so tht the block does not slip on the wedge. The force exerted by the wedge on the block has a magnitude
View SolutionA block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
View SolutionA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.

View Solution
