A body moves from point A to point B under the action of a force varying in magnitude as shown in the force displacement graph. Find total work done by the force :
10 J
50 J
60 J
40 J
The correct Answer is:D
To find the total work done by the force as a body moves from point A to point B, we can follow these steps:
Step 1: Understand the Force-Displacement Graph
The force-displacement graph shows how the force varies with displacement. The work done by a force is equal to the area under the force-displacement curve.
Step 2: Identify the Shape of the Area
From the description, we can see that the area under the curve consists of a triangle and a trapezium. We need to calculate the area of these shapes to find the total work done.
Step 3: Calculate the Area of the Triangle
The triangle is formed from the origin (0,0) to the point (5,10).
- The base of the triangle is 5 units (from 0 to 5 on the x-axis).
- The height of the triangle is 10 units (from 0 to 10 on the y-axis).
The area Atriangle can be calculated using the formula for the area of a triangle:
Atriangle=12×base×height=12×5×10=25 joules
Step 4: Calculate the Area of the Trapezium
The trapezium is formed between the points (5,10) and (7,5).
- The lengths of the parallel sides are 10 units (at x=5) and 5 units (at x=7).
- The height of the trapezium is the difference in x-coordinates, which is 7−5=2 units.
The area Atrapezium can be calculated using the formula for the area of a trapezium:
Atrapezium=12×(length of side 1+length of side 2)×height=12×(10+5)×2=12×15×2=15 joules
Step 5: Calculate Total Work Done
Now, we can find the total work done W by adding the areas of the triangle and the trapezium:
W=Atriangle+Atrapezium=25+15=40 joules
Conclusion
The total work done by the force as the body moves from point A to point B is 40 joules.
---
The force-displacement graph shows how the force varies with displacement. The work done by a force is equal to the area under the force-displacement curve.
From the description, we can see that the area under the curve consists of a triangle and a trapezium. We need to calculate the area of these shapes to find the total work done.
The triangle is formed from the origin (0,0) to the point (5,10).
- The base of the triangle is 5 units (from 0 to 5 on the x-axis).
- The height of the triangle is 10 units (from 0 to 10 on the y-axis).
Atriangle=12×base×height=12×5×10=25 joules
The trapezium is formed between the points (5,10) and (7,5).
- The lengths of the parallel sides are 10 units (at x=5) and 5 units (at x=7).
- The height of the trapezium is the difference in x-coordinates, which is 7−5=2 units.
Atrapezium=12×(length of side 1+length of side 2)×height=12×(10+5)×2=12×15×2=15 joules
Now, we can find the total work done W by adding the areas of the triangle and the trapezium:
W=Atriangle+Atrapezium=25+15=40 joules
The total work done by the force as the body moves from point A to point B is 40 joules.
Similar Questions
A body moves from point A to B under the action of a force, varying in magnitude as shown in figure. Obtain the work done. Force is expressed in newton and displacement in meter.

View SolutionA body moves from a point A to B under the action of a force shown in figure. What is the amount of work done ?

View Solution
Knowledge Check
Work will be said not to be done if the force and displacement are
AparallelBperpendicularCacting, in opposite directionDNone of these.Under the action of variable force, at any instant the displacement is
Aassumed to be infinitesimally small so that the force is assumed to be constant.Bconstant whatever be the magnitude of force.Chalf the magnitude of force.Dassumed to be infinitesimally small so that the force is assumed to be perpndicular to the displacement.
Force acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
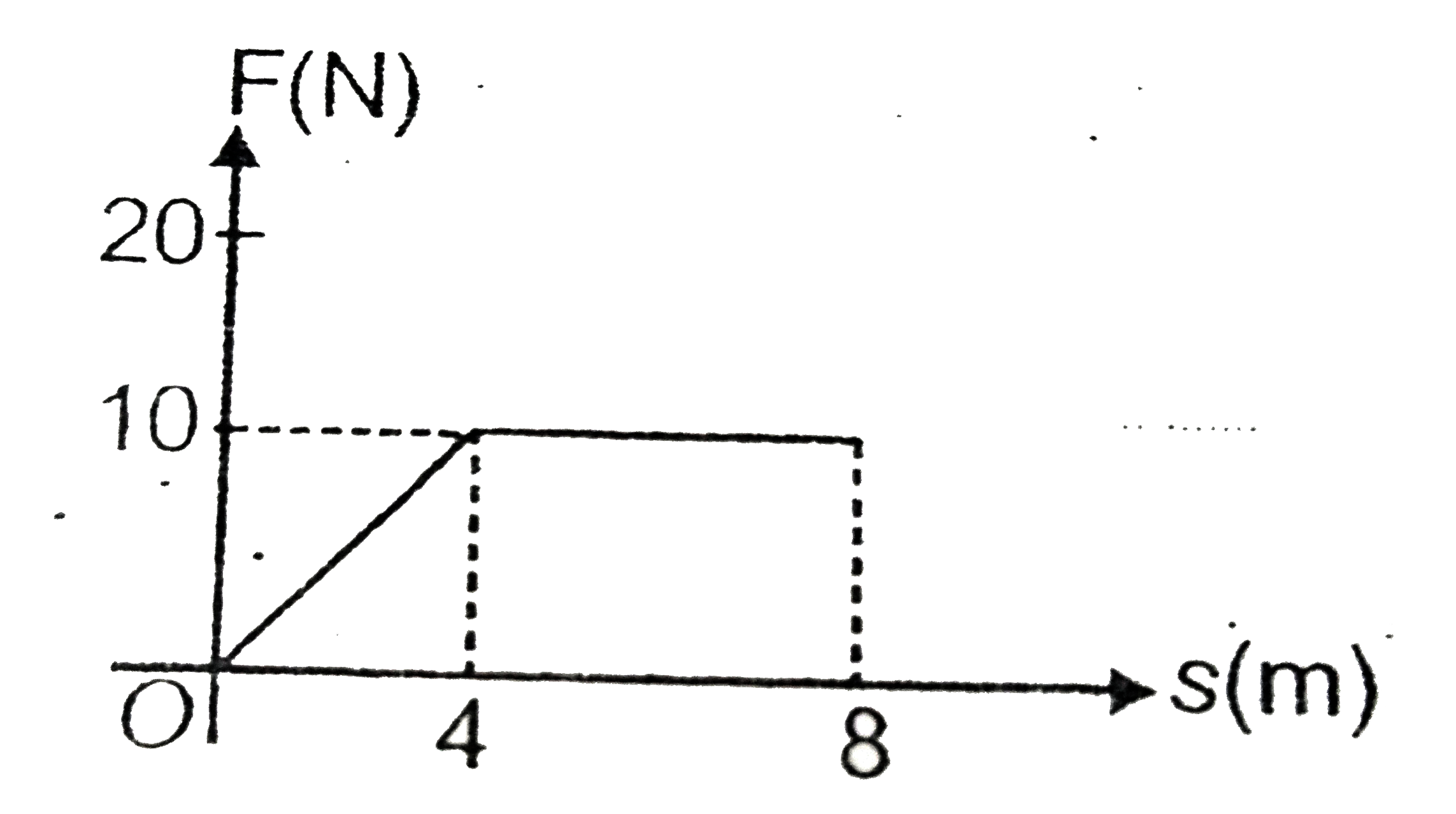
View SolutionA 5 kg block moves in a straight line on a horizontal frictionless surface under the influence of a force that varies with position as shown in the figure. Find the work done by this force as the block moves from the origin to x = 8m.
View SolutionA particle moves from a point (2 m, 3 m, 0) to (3 m, 2 m, 0) under the action of force of magnitude 5 N acting along the line y = x. The work done by the force on the particle during the displacement is
View SolutionA particle moves from a point (2m,3m,0) to (3m,2m,0) under the action of force of magnitude 5N acting along the line y=x. The work done by the force on the particle during the displacement is
View SolutionA body moves in a straight line under the action of a variable force which changes with displacement of the body as shown in the figure. What is the work done when the body has been displaced through (i) 0.2 m, (ii) 0.4 m ?

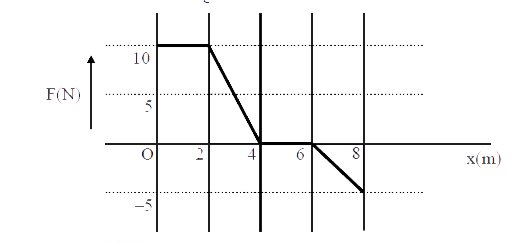
View SolutionA 10−kg block moves in a straight line under the action of a force that varies with position as shown in figure. How much work does the force do as the block moves from origin to x=8m?
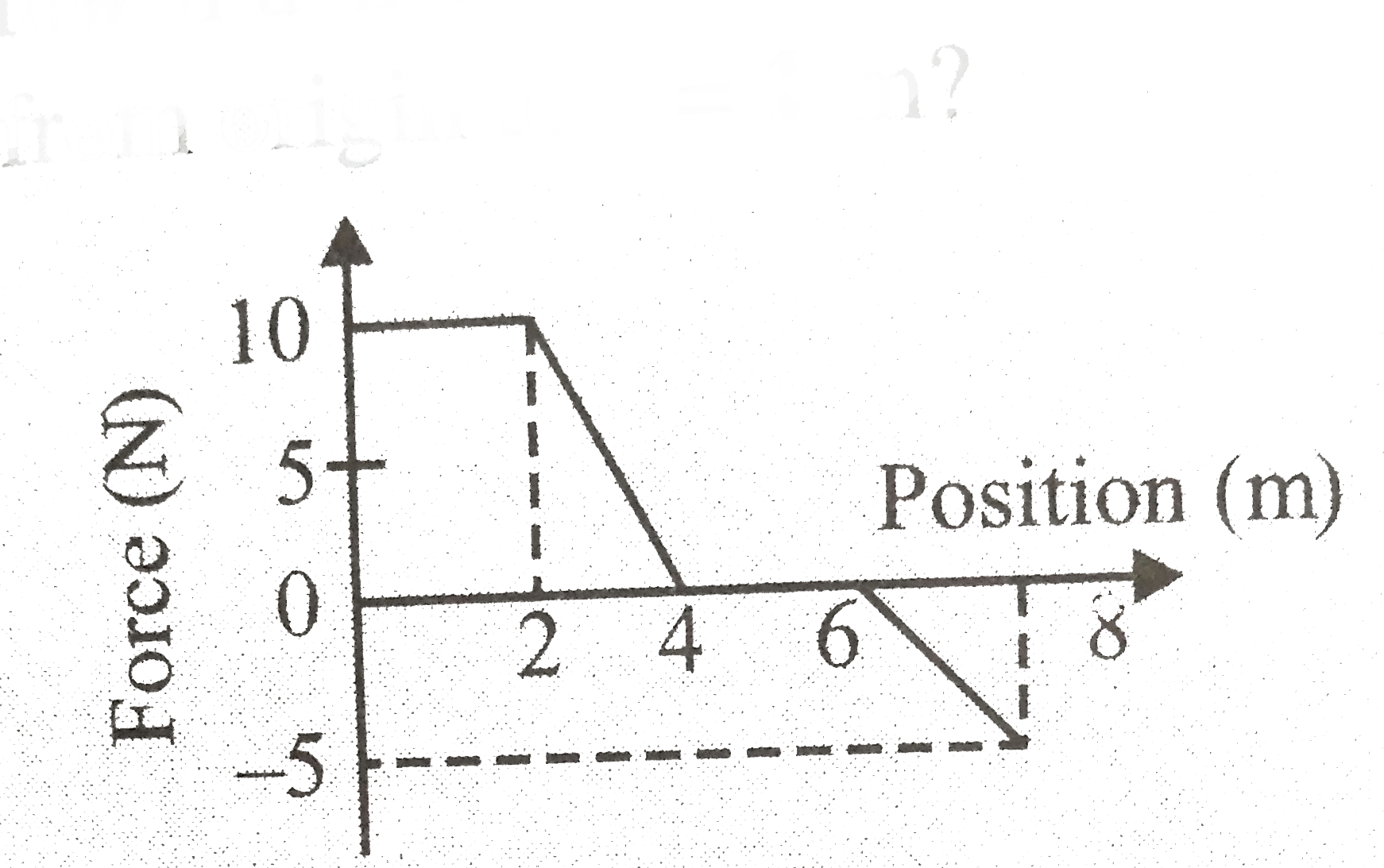
View Solution
