A particle moves from a point (2m,3m,0) to (3m,2m,0) under the action of force of magnitude 5N acting along the line y=x. The work done by the force on the particle during the displacement is
5√2 J
5√2 J
5 J
zero
To solve the problem, we need to find the work done by a force acting on a particle as it moves from one point to another. Let's break down the solution step by step.
Step 1: Identify the Initial and Final Positions
The initial position of the particle is given as Ri=(2m,3m,0) and the final position is Rf=(3m,2m,0).
Step 2: Calculate the Displacement Vector
The displacement vector →S can be calculated using the formula:
→S=→Rf−→Ri
Substituting the values:
→S=(3m−2m)^i+(2m−3m)^j+(0−0)^k
→S=1^i−1^j
Step 3: Determine the Direction of the Force
The force acts along the line y=x. This means the force can be represented as having equal components in the x and y directions. Given the magnitude of the force F=5N, the components of the force can be calculated as follows:
Fx=Fcos(45∘)=5√2andFy=Fsin(45∘)=5√2
Thus, the force vector →F can be written as:
→F=5√2^i+5√2^j
Step 4: Calculate the Work Done
The work done W by the force is given by the dot product of the force vector and the displacement vector:
W=→F⋅→S
Calculating the dot product:
W=(5√2^i+5√2^j)⋅(1^i−1^j)
W=5√2⋅1+5√2⋅(−1)
W=5√2−5√2=0
Final Answer
The work done by the force on the particle during the displacement is:
0J
The initial position of the particle is given as Ri=(2m,3m,0) and the final position is Rf=(3m,2m,0).
The displacement vector →S can be calculated using the formula:
→S=→Rf−→Ri
Substituting the values:
→S=(3m−2m)^i+(2m−3m)^j+(0−0)^k
→S=1^i−1^j
The force acts along the line y=x. This means the force can be represented as having equal components in the x and y directions. Given the magnitude of the force F=5N, the components of the force can be calculated as follows:
Fx=Fcos(45∘)=5√2andFy=Fsin(45∘)=5√2
Thus, the force vector →F can be written as:
→F=5√2^i+5√2^j
The work done W by the force is given by the dot product of the force vector and the displacement vector:
W=→F⋅→S
Calculating the dot product:
W=(5√2^i+5√2^j)⋅(1^i−1^j)
W=5√2⋅1+5√2⋅(−1)
W=5√2−5√2=0
The work done by the force on the particle during the displacement is:
0J
Topper's Solved these Questions
Similar Questions
A particle moves from a point (2 m, 3 m, 0) to (3 m, 2 m, 0) under the action of force of magnitude 5 N acting along the line y = x. The work done by the force on the particle during the displacement is
View SolutionA particle is moving from a point (2m,3m) to (1m,1m) under the influence of force with potential energy U=λ(x+y). If work done by the force is nλ, then find the value of n.
View Solution
Knowledge Check
A particle moves from point (ˆi+ˆj)m to a point (6ˆi−2ˆj)m under the action of force (10ˆi−2ˆj)N. The work done by the force is
A8 JB56 JC64 JDZeroThe displacement x in meters of a particle of mass m kg moving in one dimension under the action of a force is related to the time t in seconds by the equation t=√x+3, , the work done by the force (in J) in first six seconds is :-
A18 mBzeroC9 m/2D36 mA body of mass 0.5 kg travels in a straight line with velocity v=5x3/2. The work done by the net force during its displacement from x=0 to x=2 m is
A50JB45JC25JDnone of these
A particle moves rom a point →r1=(2m)→i+(3m)→j to another point →r2=(3m)→i+(2m)→j during which a certain force →F(5N)→i+(5N)→j acts on it. Fikd the work doen by the force on the particle during the displcement.
View SolutionAn object is displaced from point A(2m,3m,4m) to a point B(1m,2m,3m) under a constant force F=(2ˆi+3ˆj+4ˆk)N. Find the work done by this force in this process.
View SolutionForce F on a particle moving in a straight line varies with distance d as shown is figure. The work done on the particle during its displacement of 10 m is :-
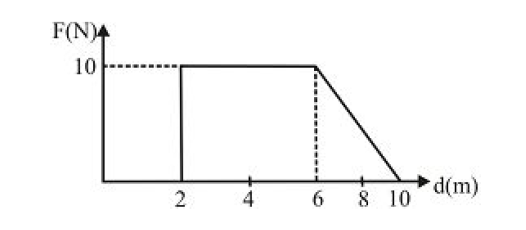
View SolutionA force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View SolutionA force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
View Solution
