If a projectile is projected with initial speed u and angle θ from horizontal then what will be its average power up to time when it will hit the ground again ?
100
200
300
0
The correct Answer is:D
To find the average power of a projectile projected with an initial speed u at an angle θ when it hits the ground again, we can follow these steps:
Step 1: Understand the Concept of Power
Power is defined as the rate of doing work. Mathematically, it can be expressed as:
P=WT
where W is the work done and T is the time taken.
Step 2: Analyze the Forces Acting on the Projectile
In projectile motion, the only force acting on the projectile (after it is launched) is the gravitational force mg acting downwards. In the horizontal direction, there is no force acting on the projectile (assuming no air resistance).
Step 3: Determine the Displacement
When the projectile is launched and returns to the ground, the vertical displacement y is zero because it starts and ends at the same height. Therefore, the total work done in the vertical direction is:
Wy=Fy⋅dy=mg⋅0=0
where dy is the vertical displacement.
Step 4: Calculate the Average Power in the Vertical Direction
Since the vertical displacement is zero, the average velocity in the vertical direction is also zero:
Average Velocity in y=Total Displacement in yTotal Time=0T=0
Thus, the average power in the vertical direction is:
Pavg,y=Fy⋅Average Velocity in y=mg⋅0=0
Step 5: Analyze the Horizontal Motion
In the horizontal direction, the projectile moves with a constant velocity ucosθ since there is no horizontal force acting on it. However, since there is no work done in the horizontal direction (as the displacement is not changing the height), the average power in the horizontal direction is also zero:
Pavg,x=0
Step 6: Combine the Results
Since both the average power in the vertical direction and the horizontal direction are zero, the total average power is:
Pavg=Pavg,x+Pavg,y=0+0=0
Final Answer
The average power of the projectile up to the time it hits the ground again is:
0
Power is defined as the rate of doing work. Mathematically, it can be expressed as:
P=WT
where W is the work done and T is the time taken.
In projectile motion, the only force acting on the projectile (after it is launched) is the gravitational force mg acting downwards. In the horizontal direction, there is no force acting on the projectile (assuming no air resistance).
When the projectile is launched and returns to the ground, the vertical displacement y is zero because it starts and ends at the same height. Therefore, the total work done in the vertical direction is:
Wy=Fy⋅dy=mg⋅0=0
where dy is the vertical displacement.
Since the vertical displacement is zero, the average velocity in the vertical direction is also zero:
Average Velocity in y=Total Displacement in yTotal Time=0T=0
Thus, the average power in the vertical direction is:
Pavg,y=Fy⋅Average Velocity in y=mg⋅0=0
In the horizontal direction, the projectile moves with a constant velocity ucosθ since there is no horizontal force acting on it. However, since there is no work done in the horizontal direction (as the displacement is not changing the height), the average power in the horizontal direction is also zero:
Pavg,x=0
Since both the average power in the vertical direction and the horizontal direction are zero, the total average power is:
Pavg=Pavg,x+Pavg,y=0+0=0
The average power of the projectile up to the time it hits the ground again is:
0
Similar Questions
Knowledge Check
A particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
AucosθsecαBusecθcosαCucosθtanαDucosθcotαA projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
Aucosθ2BucosθCu(2cos(θ)2−sec(θ)2)Du(cos(θ)2−sec(θ)2)A projectile is projected with linear momentum p making angle θ with the horizontal. The change in momentum of the projectile on returning to the ground will be-
A2pB2pcosθC2psinθD2ptanθ
What is the average velocity of a particle projected from the ground with speed u at an angle alpha with horizontal over a time interval from beginning till it strikes the ground again?
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : time of flight.
View SolutionFor a projectile first with velocity u at an angle θ with the horizontal.

View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
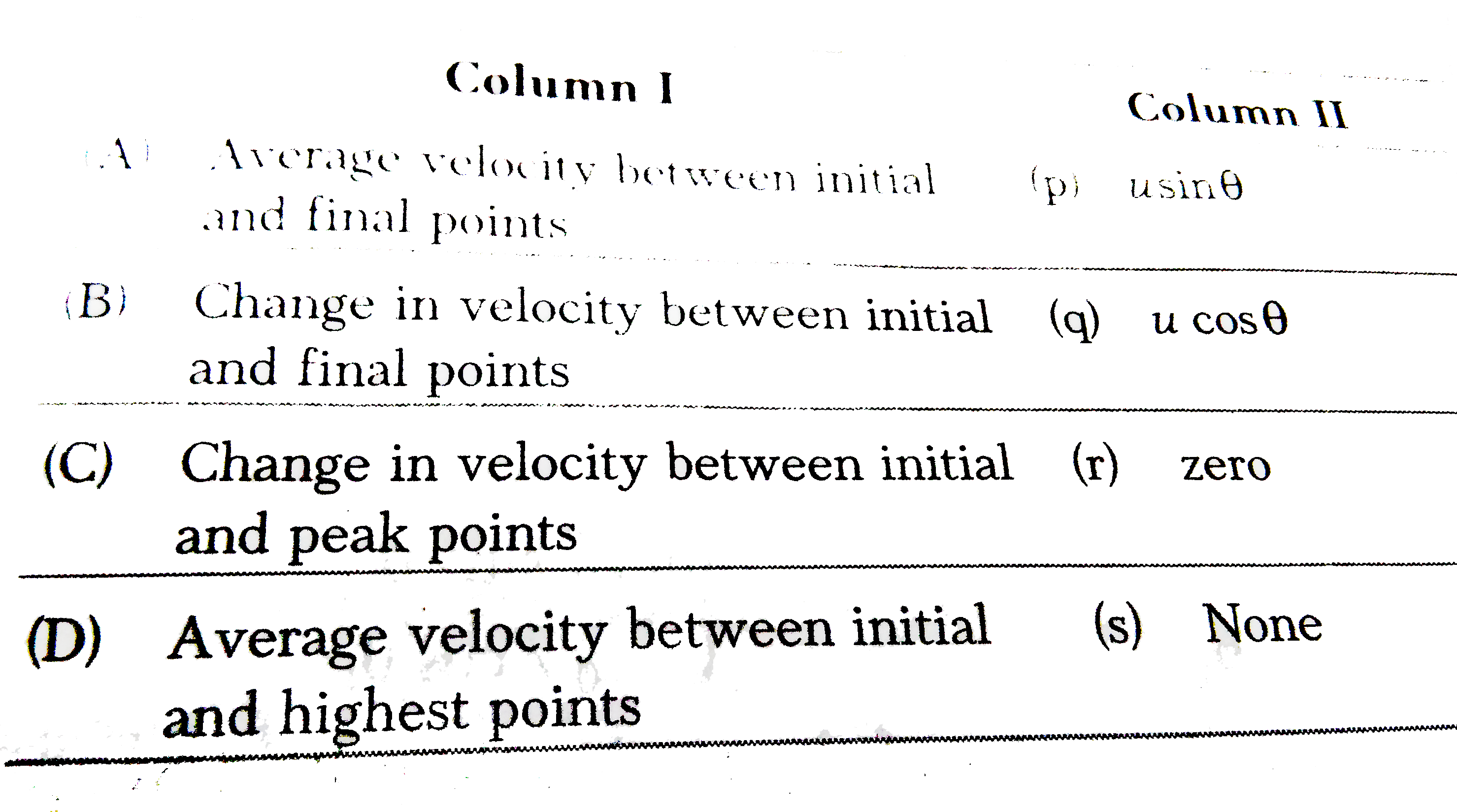
View SolutionA projectile is projected with speed u at an angle θ with the horizontal . The average velocity of the projectile between the instants it crosses the same level is
View Solution