A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
mgM+m
2mgM+m
2mgM+2m
2mg2M+m
The correct Answer is:C
To find the linear acceleration of the bucket suspended from the solid cylinder, we can follow these steps:
Step 1: Analyze the Forces Acting on the Bucket
The forces acting on the bucket of mass m are:
- The gravitational force acting downwards: Fg=mg
- The tension T in the rope acting upwards.
Using Newton's second law, we can write the equation for the bucket:
mg−T=ma(1)
where a is the linear acceleration of the bucket.
Step 2: Analyze the Torque on the Cylinder
The tension T in the rope creates a torque τ on the cylinder. The torque can be expressed as:
τ=T⋅R
where R is the radius of the cylinder.
Step 3: Relate Torque to Angular Acceleration
The torque is also related to the angular acceleration α of the cylinder by the equation:
τ=I⋅α
where I is the moment of inertia of the cylinder. For a solid cylinder, the moment of inertia is given by:
I=12MR2
Thus, we can write:
T⋅R=12MR2⋅α(2)
Step 4: Relate Linear Acceleration to Angular Acceleration
The linear acceleration a of the bucket is related to the angular acceleration α of the cylinder by the equation:
a=R⋅α
From this, we can express α as:
α=aR(3)
Step 5: Substitute α into the Torque Equation
Substituting equation (3) into equation (2):
T⋅R=12MR2⋅aR
This simplifies to:
T=12Ma(4)
Step 6: Substitute T into the Bucket's Equation
Now, substitute equation (4) into equation (1):
mg−12Ma=ma
Rearranging gives:
mg=ma+12Ma
Factoring out a:
mg=a(m+12M)
Step 7: Solve for the Linear Acceleration a
Now, we can solve for a:
a=mgm+12M
Final Result
The linear acceleration of the bucket is:
a=mgm+12M
---
The forces acting on the bucket of mass m are:
- The gravitational force acting downwards: Fg=mg
- The tension T in the rope acting upwards.
mg−T=ma(1)
where a is the linear acceleration of the bucket.
The tension T in the rope creates a torque τ on the cylinder. The torque can be expressed as:
τ=T⋅R
where R is the radius of the cylinder.
The torque is also related to the angular acceleration α of the cylinder by the equation:
τ=I⋅α
where I is the moment of inertia of the cylinder. For a solid cylinder, the moment of inertia is given by:
I=12MR2
Thus, we can write:
T⋅R=12MR2⋅α(2)
The linear acceleration a of the bucket is related to the angular acceleration α of the cylinder by the equation:
a=R⋅α
From this, we can express α as:
α=aR(3)
Substituting equation (3) into equation (2):
T⋅R=12MR2⋅aR
This simplifies to:
T=12Ma(4)
Now, substitute equation (4) into equation (1):
mg−12Ma=ma
Rearranging gives:
mg=ma+12Ma
Factoring out a:
mg=a(m+12M)
Now, we can solve for a:
a=mgm+12M
The linear acceleration of the bucket is:
a=mgm+12M
Similar Questions
A cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination θ. Calculate the linear acceleration of the axis of cylinder.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform solid cylinder of mass M and of radius R rotates about a frictionless axle. Two masses are suspended from a rope wrapped arround the cylinder. If the system is released from rest, the tension in each rope is?
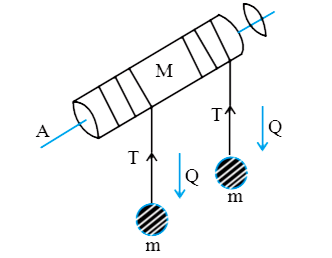 AMmgM+mBMmgM+2mCMmgM+3mDMmgM+4m
AMmgM+mBMmgM+2mCMmgM+3mDMmgM+4m - Question 2 - Select One
A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
A4mgM+2mB4mgM+4mC2mgM+mD2mgM+2m - Question 3 - Select One
A uniform disc of mass M and radius R is mounted on an axle supported in frictionless bearings. A light cord is wrapped around the rim of the disc and a steady downward pull T is exerted on the cord. The angular acceleration of the disc is
ATMRBMRTC2TMRDMR2T
A solid cylinder of mass M and radius R has a light thin tape wound around it as shown in the figure. The tape passes over a light, smooth fixed pulley to a block of mass m. Find the linear acceleration of the cylinder's axis up the incline (in) assuming no slipping. Given mass of the block = 1.5Kg, mass of the cylinder = 2 kg, the angle inclination = 30° and take g=10ms−2
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
 View Solution
View Solution

