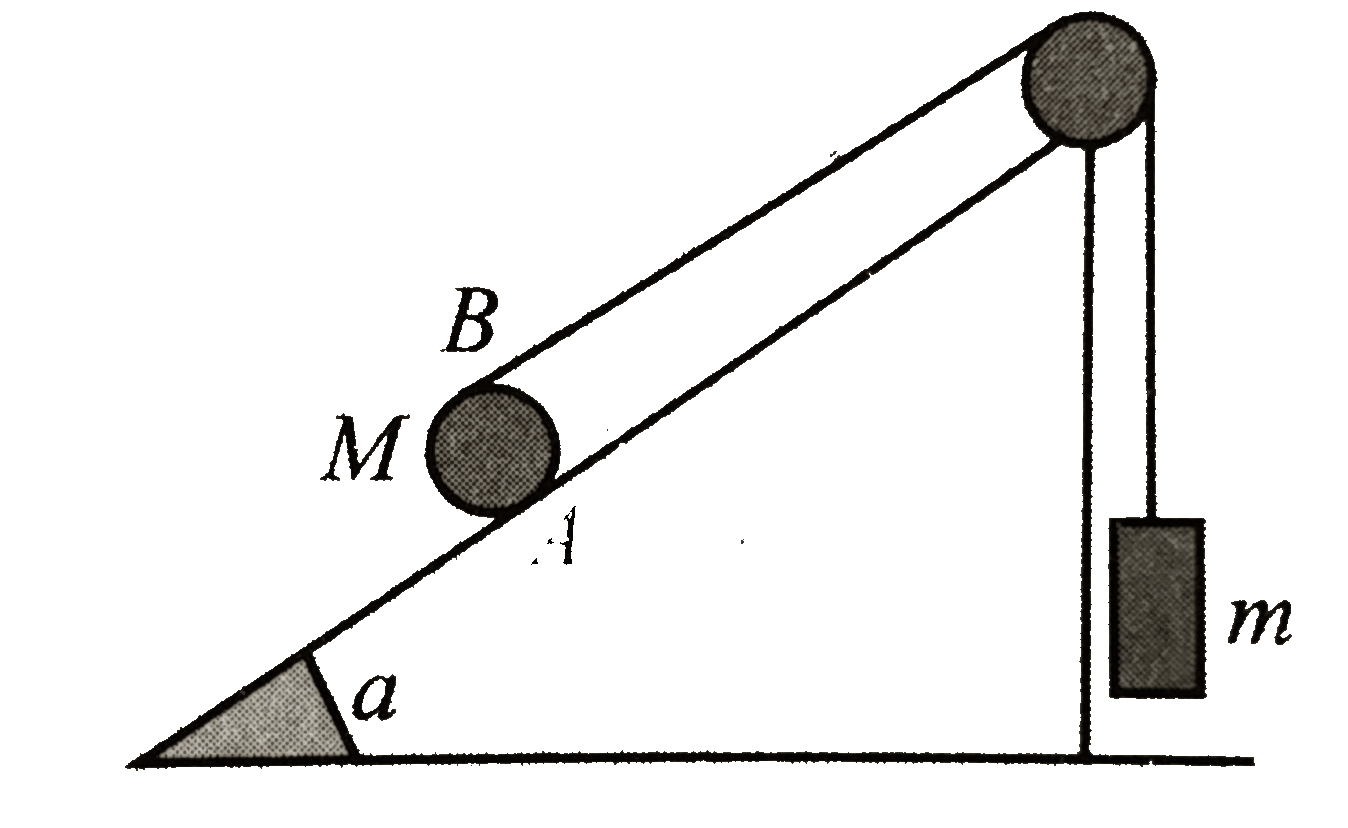
A solid cylinder of mass M and radius R has a light thin tape wound around it as shown in the figure. The tape passes over a light, smooth fixed pulley to a block of mass m. Find the linear acceleration of the cylinder's axis up the incline (in) assuming no slipping. Given mass of the block = 1.5Kg, mass of the cylinder = 2 kg, the angle inclination = 30° and take g=10ms−2
Step by step video & image solution for A solid cylinder of mass M and radius R has a light thin tape wound around it as shown in the figure. The tape passes over a light, smooth fixed pulley to a block of mass m. Find the linear acceleration of the cylinder's axis up the incline (in) assuming no slipping. Given mass of the block = 1.5Kg, mass of the cylinder = 2 kg, the angle inclination = 30° and take g= 10 ms^(-2) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Find the tension in the tape and the linear acceleration of the cylinder up the incline, assuming there is no slipping. (TakeM=4m and g=10m/s2)
 View Solution
View SolutionA rope of negligible mass is wound around a hollow cylinder of mass 3kg and radius 40cm. What is the angular acceleration of the cylinder, if the rope is pulled with a force of 30N ? What is the linear acceleration of the rope ? Assume that there is no slipping.
View Solution
Knowledge Check
- Question 1 - Select One
A rope is wound round a hollow cylinder of mass 2 kg and radius 0.5 m. If the rope is pulled with a force of 80 N, the angular acceleration of the cylinder will be -
A20 rad/s2B40 rad/s2C60 rad/s2D80 rad/s2 - Question 2 - Select One
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
A√34ghB√43ghC√4ghD√2gh - Question 3 - Select One
A solid cylinder of mass M and of radius R is fixed on a frictionless axle over a well. A rope negligible mass is wrapped around the cylinder. A bucket of uniform mass m is suspended from it. The linear acceleration bucket will:
AmgM+mB2mgM+mC2mgM+2mD2mg2M+m
A solid cylinder of mass m and radius R rest on a plank of mass 2m lying on a smooth horizontal surface. String connecting cylinder to the plank is passing over a massless pulley mounted on a movable light block B and the friction between the cylinder and the plank is sufficient to prevent slipping. if the block B is pulled with a constant forceF, the acceleration of the plank is 2Fxm then calculate x.
 View Solution
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View SolutionA solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA string is warapped around a cylinder of mass m and radius r. The string is also connected to a block of same mass m with the help of another pulley as shown in figure. The angular acceleration of the cylinder is ( friction is sufficient for rolling ) ( all pulleys are ideal)
 View Solution
View Solution
