Mutual inductance of two coils depends on their self inductance L1 and L2 as :
M12=L1/L2
M12=L2/L1
M12=√L1L2
M12=√L1/L2
The correct Answer is:C
To find the relationship between the mutual inductance M of two coils and their self-inductances L1 and L2, we can follow these steps:
Step 1: Define the Self-Inductance
The self-inductance L1 of the first coil is defined as the ratio of the magnetic flux Φ11 linked with the first coil due to its own current I1:
Φ11=L1I1
Step 2: Define the Mutual Inductance
The mutual inductance M is defined as the ratio of the magnetic flux Φ12 linked with the first coil due to the current I2 in the second coil:
Φ12=MI2
Step 3: Write the Flux Relationships
For the second coil, we can similarly define the self-inductance L2 and the mutual inductance M:
Φ21=MI1(flux in the second coil due to the first coil)
Φ22=L2I2(self-flux in the second coil)
Step 4: Set Up the Equations for Maximum Flux Linkage
At maximum flux linkage, the self-flux in each coil is equal to the mutual flux due to the other coil:
Φ11=Φ12⇒L1I1=MI2(1)
Φ22=Φ21⇒L2I2=MI1(2)
Step 5: Multiply the Two Equations
Now, we multiply equations (1) and (2):
(L1I1)(L2I2)=(MI2)(MI1)
This simplifies to:
L1L2I1I2=M2I1I2
Step 6: Cancel Common Terms
Assuming I1 and I2 are not zero, we can cancel I1I2 from both sides:
L1L2=M2
Step 7: Solve for Mutual Inductance
Taking the square root of both sides gives us the expression for mutual inductance:
M=√L1L2
Final Result
Thus, the mutual inductance M of the two coils depends on their self-inductances L1 and L2 as:
M=√L1L2
---
The self-inductance L1 of the first coil is defined as the ratio of the magnetic flux Φ11 linked with the first coil due to its own current I1:
Φ11=L1I1
The mutual inductance M is defined as the ratio of the magnetic flux Φ12 linked with the first coil due to the current I2 in the second coil:
Φ12=MI2
For the second coil, we can similarly define the self-inductance L2 and the mutual inductance M:
Φ21=MI1(flux in the second coil due to the first coil)
Φ22=L2I2(self-flux in the second coil)
At maximum flux linkage, the self-flux in each coil is equal to the mutual flux due to the other coil:
Φ11=Φ12⇒L1I1=MI2(1)
Φ22=Φ21⇒L2I2=MI1(2)
Now, we multiply equations (1) and (2):
(L1I1)(L2I2)=(MI2)(MI1)
This simplifies to:
L1L2I1I2=M2I1I2
Assuming I1 and I2 are not zero, we can cancel I1I2 from both sides:
L1L2=M2
Taking the square root of both sides gives us the expression for mutual inductance:
M=√L1L2
Thus, the mutual inductance M of the two coils depends on their self-inductances L1 and L2 as:
M=√L1L2
Similar Questions
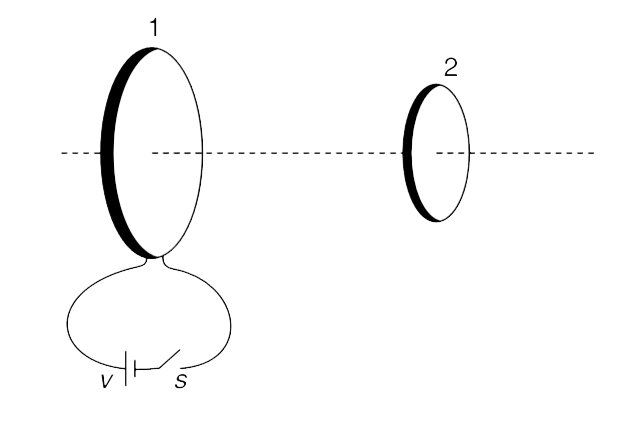
Two coils – 1 and 2 – are mounted co axially as shown in the figure. The resistance of the two coils are R1 and R2 and their self inductances are L1 and L2 respectively. Switch S is closed at time t = 0 to connect the coil 1 to an ideal cell of emf V. It is observed that by the time current reaches its steady value in coil 1, the quantity of charge that flows in coil 2 is Q0. Calculate the mutual inductance (M) between the two coils.
View SolutionMutual inductance & L-C oscillations
View Solution
Knowledge Check
The mutual inductance of coil does not depend on
Anumber of turns of the coilBgeometrical properties of the coilCpermebility of the mediumDall of the aboveMutual inductance of two coils can be increased by
Adecreasing the number of turns on the coilsBincreasing the number of turns on the coilsCwinding the coils on the wooden coreDnone of these.Mutual inductance of two coils can be increased by
ADecreasing the number of turns in the coilsBIncreasing the number of turns in the coilsCWinding the coils on wooden coreDNone of the above
An oscillating circuit consists of two coils connected in series whose inductances are L1 and L2 active resistances are R1 and R2 , and mutual inductance is negligible. These coils are to be replaced by one, keeping the frequency and the quality factor of the circuit constant. Find the inductance and the active resistance of such a coil.
View SolutionAssertion :- The mutual inductance M between two coils of self inductances L1andL2 is given by M>√L1L2
Reason :- The energy density (i.e. energy per unit volume) at an poit, where the magnetic field B is given by B22μ0
View Solutionthe dimension of self inductance L are
View Solutionthe dimension of self inductance L are
View SolutionThe inductors of self inductance L1 and L2 are put in series .
View Solution
