One mole of a monatomic ideal gas is taken through the cycle shown in figure.

A B adiabatic , expansion
cooling at constant volume
adiabatic compression
heating at constant volume
The pressure and temperature at A,B etc. are denoted by , ...., ,...., etc. respectively. Given that
and .
Calculate the following quantities :
The temperature
For path AB
or …(3.125)
For path BC
or ….(3.126)
For path CD
...(3.127)
For path AD ....(3.128)
Dividing equation-(3.125) by(3.127), we get
..(3.129 )
Dividing equation-(3.128) by equation-(3.126) we get
or ...(3.130)
From equation-(3.129) and (3.130)
=500 K
Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Discussion Question
17 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Conceptual MCQs Single Option Correct
21 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems
42 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
Similar Questions
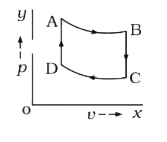
One mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion

B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The work done by the gas in process A→B (in J)
View Solution
The pressure at C is
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
B→C: cooling at constant volume
C→D adiabatic compression D→A: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The temperature TD (in K) [Given : (25)2/5=0.85 ]
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion

B→C: cooling at constant volume
C→D adiabatic compression D→A: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The temperature TD (in K) [Given : (25)2/5=0.85 ]
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume
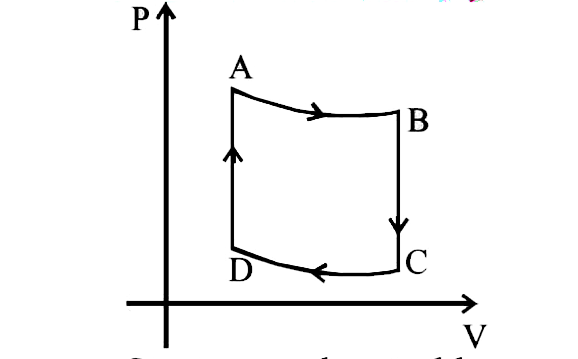
The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume

The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
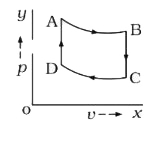
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion

B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
_E01_271_Q01.png)
View SolutionOn mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
<
View Solution
