In the polytropic process PV2 = constant, is the gas cooled'or heated with increase in volume.
To determine whether the gas cools or heats with an increase in volume during a polytropic process defined by the equation PV2=constant, we can follow these steps:
1. Understand the Polytropic Process:
The given equation PV2=constant indicates a polytropic process where the product of pressure P and the square of volume V remains constant.
2. Express Pressure in Terms of Volume:
From the ideal gas law, we know that:
PV=nRT
Rearranging this gives us:
P=nRTV
3. Substitute Pressure into the Polytropic Equation:
Substitute the expression for P into the polytropic equation:
(nRTV)V2=constant
Simplifying this yields:
nRTV=constant
4. Analyze the Relationship Between Volume and Temperature:
From the equation nRTV=constant, we can express it as:
TV=constantnR
This shows that T (temperature) is inversely proportional to V (volume):
T∝1V
5. Determine the Effect of Increasing Volume:
If the volume V increases, the temperature T must decrease to keep the product TV constant. Therefore, as V increases, T decreases.
6. Conclusion:
Since the temperature of the gas decreases when the volume increases, we conclude that the gas cools down during this process.
Final Answer:
The gas cools with an increase in volume in the polytropic process defined by PV2=constant.
---
The given equation PV2=constant indicates a polytropic process where the product of pressure P and the square of volume V remains constant.
From the ideal gas law, we know that:
PV=nRT
Rearranging this gives us:
P=nRTV
Substitute the expression for P into the polytropic equation:
(nRTV)V2=constant
Simplifying this yields:
nRTV=constant
From the equation nRTV=constant, we can express it as:
TV=constantnR
This shows that T (temperature) is inversely proportional to V (volume):
T∝1V
If the volume V increases, the temperature T must decrease to keep the product TV constant. Therefore, as V increases, T decreases.
Since the temperature of the gas decreases when the volume increases, we conclude that the gas cools down during this process.
The gas cools with an increase in volume in the polytropic process defined by PV2=constant.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Conceptual MCQs Single Option Correct21videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Numerical MCQs Single Options Correct42videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.411videos
THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems42videos
PHOTOELECTRIC EFFECT AND MATTER WAVES
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems28videos
WAVE OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
One mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
ARΔTB3RΔTC5RΔTD6RΔT - Question 2 - Select One
P-V graph for an ideal gas undergoing polytropic process PVm=constant is shown here. Find the value of m.
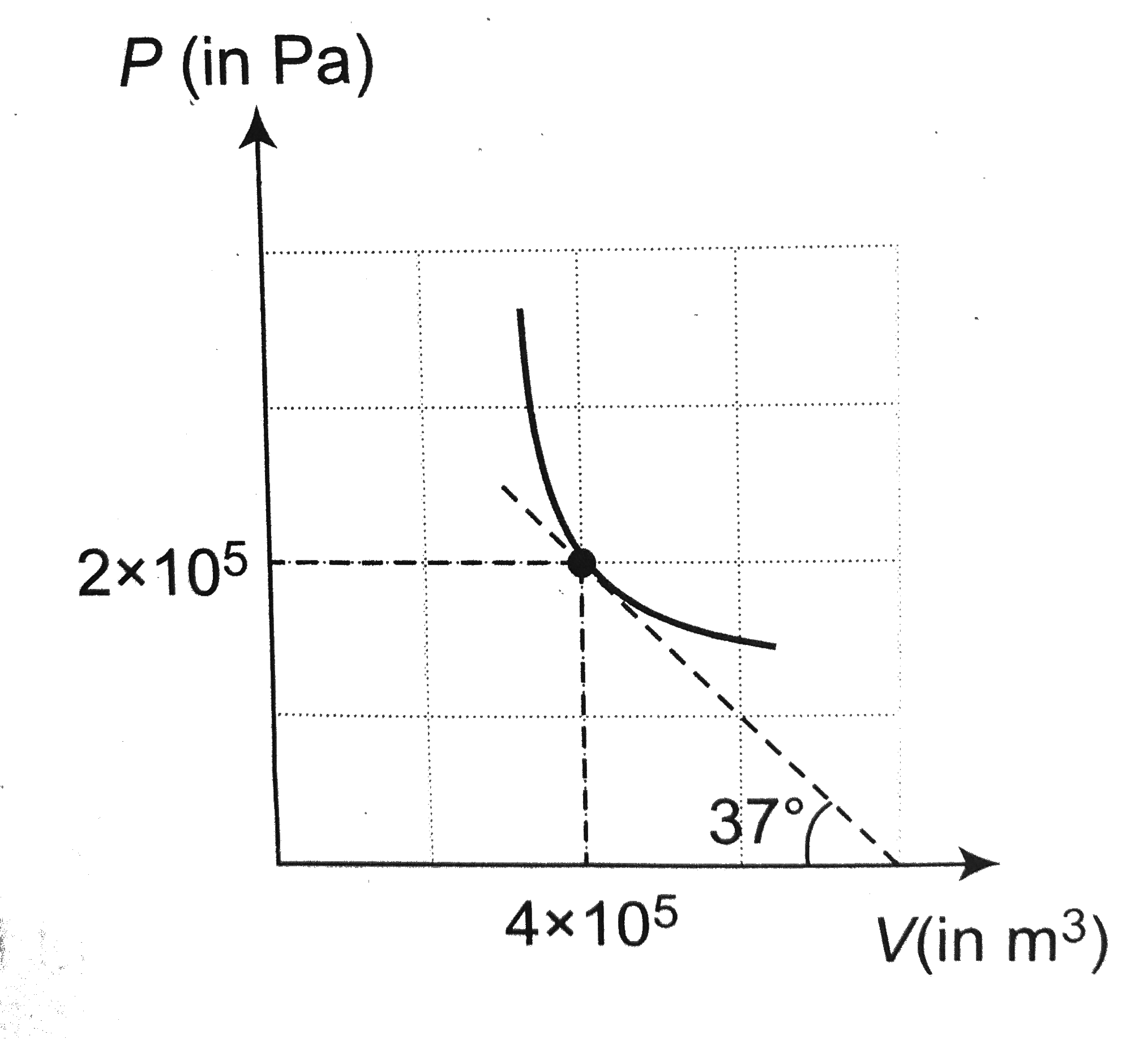 A34B−32C53D32
A34B−32C53D32 - Question 3 - Select One or More
In the process pV2= constant, if temperature of gas is increased, then
A(a) change in internal energy of gas is positiveB(b) work done by gas is positiveC(c) heat is given to the gasD(d) heat is taken out from the gas
A gas expands in such a manner that its pressure and volume comply with the condition PV2 = constant. Will the gas cool or get heated on expansion?
View SolutionA certain ideal gas undergoes a polytropic process PVn = constant such that the molar specific heat during the process is negative. If the ratio of the specific heats of the gas be γ, then the range of values of n will be
View SolutionFigure demonstrates a polytropic process (i.e.PVn = constant ) for an ideal gas. The work done by the gas be in the process AB is
_S01_086_Q01.png) View Solution
View Solution1 mole of an ideal diatomic gas undergoes a reversible polytropic process (PV2=constant). The gas expand from initial volume of 1 litre and temp 300K to final volume 3 lit. Claculate change in internal energy (approx).
View SolutionFor polytropic process PVn = constant, molar heat capacity (Cm) of an ideal gas is given by:
View Solution

