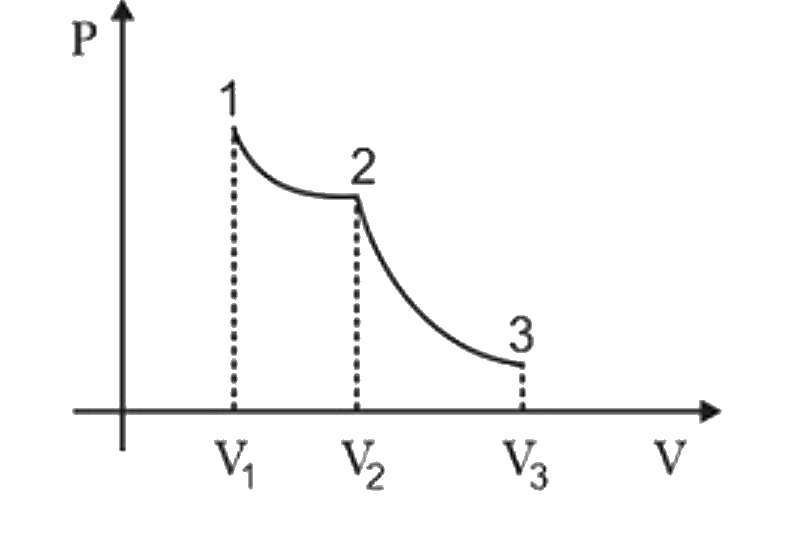
A gass of given mass at a pressure of 105Nm−2 expands isothermally until its volume is doubled and then adiabatically until volume is again double. Find the final pressure of the gas. (γ=1.4)
The correct Answer is:1.89×104Nm−2
Step by step video, text & image solution for A gass of given mass at a pressure of 10^(5)Nm^(-2) expands isothermally until its volume is doubled and then adiabatically until volume is again double. Find the final pressure of the gas. (gamma=1.4) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.1
6 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Practice Exercise 3.3
10 Videos
- THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - THERMODYNAMICS LAWS & SPECIFIC HEATS OF GASES EXERCISE - Advance MCQs with One or More Options Correct
10 Videos
- PHOTOELECTRIC EFFECT AND MATTER WAVESBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - PHOTOELECTRIC EFFECT AND MATTER WAVESEXERCISE - Unsolved numerical problems
42 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
Similar Questions
One mole of perfect gas, initially at a pressure and temperture of 105Nm−2 and 300 K, respectively, expands isothermally until its volume is doubled and then adiabatically until its volume is again doubled. Find the final pressure of the gas. Given γ=1.4.
View SolutionA litre of hydrogen at 127∘C and 106dy≠cm−2 pressure expands isothermally until its volume is doubled and then adiabatically until its volume is redoubled. Find the final pressure of the gas. Given γ=1.4.
View Solution
Knowledge Check
A monatomic gas at a pressure P, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is ( take γ=53)
A64 PB32 PCP/64D16 PA monatomic gas at a pressure P, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is ( take γ=53)
A64 PB32 PCP64D16 PA monoatomic gas at a pressure P, having a volume V expands isothermally to a volume 2V and then adiabatically to a volume 16 V. The final pressure of the gas is (Take γ=5/3)
A64 PB32 PCP/64D16 P
A certain volume of a gas (diatomic) expands isothermally at 20∘C until its volume is doubled and then adiabatically until its volume is again doubled. Find the final temperature of the gas, given γ= 1.4 and that there is 0.1 mole of the gas. Also calculate the work done in the two cases. R=8.3Jmole−1K−1
View SolutionA certain volume of a gas (diatomic) expandds isothermally at 20∘C until its volume is doubled and then adiabatically until its volume is again doubled. Find the final temperature of the gas, given γ=1.4 and that there is 0.1 mole of the gas. Also calculate the work done in the two cases. R=8.3Jmole−1K−1
View SolutionOne mole of a perfect gas, initally at a pressure and temperature of 105N/m2 and 300 K, respectively, expands isothermally unitl its volume is doubled and then adiabatically until its volume is again doubled. Find final pressure and temperature of the gas Find the total work done during the isothermal and adiabatic processes. Given γ=1.4. Also draw the P-V diagram for the process.

View SolutionA certain volume of a gas (diatomic) expands isothermally at 20∘C until its volume is doubled and then adiabatically until its volume is again doubled. Find the final temperature of the gas, given g=1.4 and that there is 0.1mo≤ of the gas. Also calculate the work done in the two coses R=8.3Jmo≤−1K−1
View SolutionA monatomic gas at a pressure P, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is ( take γ=53)
View Solution
