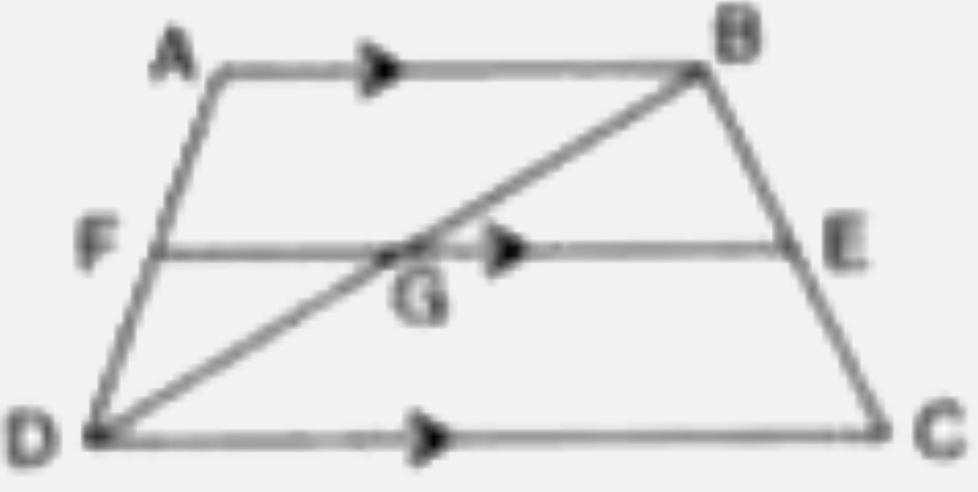
In a trapezium ABCD, AB||DC and DC=2AB. EF drawn parallel to AB cuts AD in F and BC in E such that BEBC=34 .Diagonals DB intersects EF at G. Prove that 7EF=10AB.
In △{DF}G and △{DAB}, we have
∠1=∠2 [∵{AB}∣{DC}m∴∠1 and ∠2 are corresponding angles ]
∠{FDG}=∠{ADB} [{Common}]
So, by AA-criterion of similarity, we have
∴△{DFG}sim△{DAB}
⇒{DF}{DA}={FG}{AB}......({i})
In trapezium {ABCD}, we have
{EF}|{AB}|{D}
∴{AF}{DF}={BE}{EC}
⇒{AF}{DF}=34
[∵{BE}{EC}=34( Given )]
⇒{AF}{DF}+1=34+1
[Adding 1 on both sides]
⇒{AF}+{DF}{DF}=74
⇒{AD}{DF}=74
⇒{DF}{AD}=47...... (ii)
From (i) and (ii), we get
{FG}{AB}=47
⇒{FG}=47{AB}........({iii})
In △BEG and △BCD, we have
∠{BEG}=∠{BCD} [Corresponding angles]
∠{B}=∠{B} [ Common]
∴△{BEG}sim△{BCD} [{By}{∀}-criterion of similarity]
⇒{BE}{BC}={EG}{CD}
⇒37={EG}{CD} [∵{BE}{EC}=34⇒{EC}{BE}=43⇒{EC}{BE}+1=43+1⇒{BC}{BE}=73]
⇒{EG}=37{CD}
⇒{EG}=37×2{AB}
⇒{EG}=67×{AB}
Adding (iii) and (iv), we get
{FG}+{EG}=47{AB}+67{AB}
⇒{EF}=107{AB}
⇒7{EF}=10{AB} [Hence proved]
Similar Questions
In trapezium ABCD, AB || DC. E and F are points on non-parallel sides AD and BC respectively such that EF || AB. Show that AEED=BFFC
View SolutionABCD is a trapezium with AB∣∣DC. E and F are points on non-parallel sides AD and BC respectively such that EF is parallel to AB (see the figure). Show that AEED=BFFC

View SolutionIn a trapezium ABCD, AB∣∣AD and DC=2AB. EF∣∣AB, cuts AD in F and BC in E such that BEEC=34. Diagonal DB intersects EF at G. Prove that, 7EF=10AB.
View Solutionएक समलम्ब चतुर्भुज ABCD में AB∣∣DC और DC=2AB, यहाँ AB के समान्तर EF रेखा खींची गई हैं जो AD को F तथा BC को E बिंदु पर काटती हैं, तथा यदि BEEC=34 | विकर्ण DB रेखाखण्ड EF को बिंदु G पर प्रतिच्छेद करता हैं , तो सिद्ध कीजिए कि 8FE=10AB |
View Solutionआकृति में, ABCD एक समलम्ब चतुर्भुज हैं, जिसमें भुजा AB भुजा DC के समान्तर हैं तथा E भुजा AD का मध्य-बिंदु हैं। E भुजा BC पर इस प्रकार है खंड EF, भुजा DC के समान्तर हैं। सिद्ध कीजिए कि EF=12(AB+DC)
View SolutionOf the trapezium ABCD, AB∣∣DC and DC = 2AB. If the line segment EF drawn parallel to AB meets AD and BC at the points Fand E respectively so that (BE)/(EC)=3/4 and the diagonal DB meets EF at the points G, prove that 7FE=11AB
View SolutionIn trapezium ABCD, AB/DC and DC=2 AB. EF, drawn parallel to AB cuts AD in F and BC in E such that 4BE= 3 EC. Diagonal DB intersects FE at point G. Prove that: 7EF= 10AB
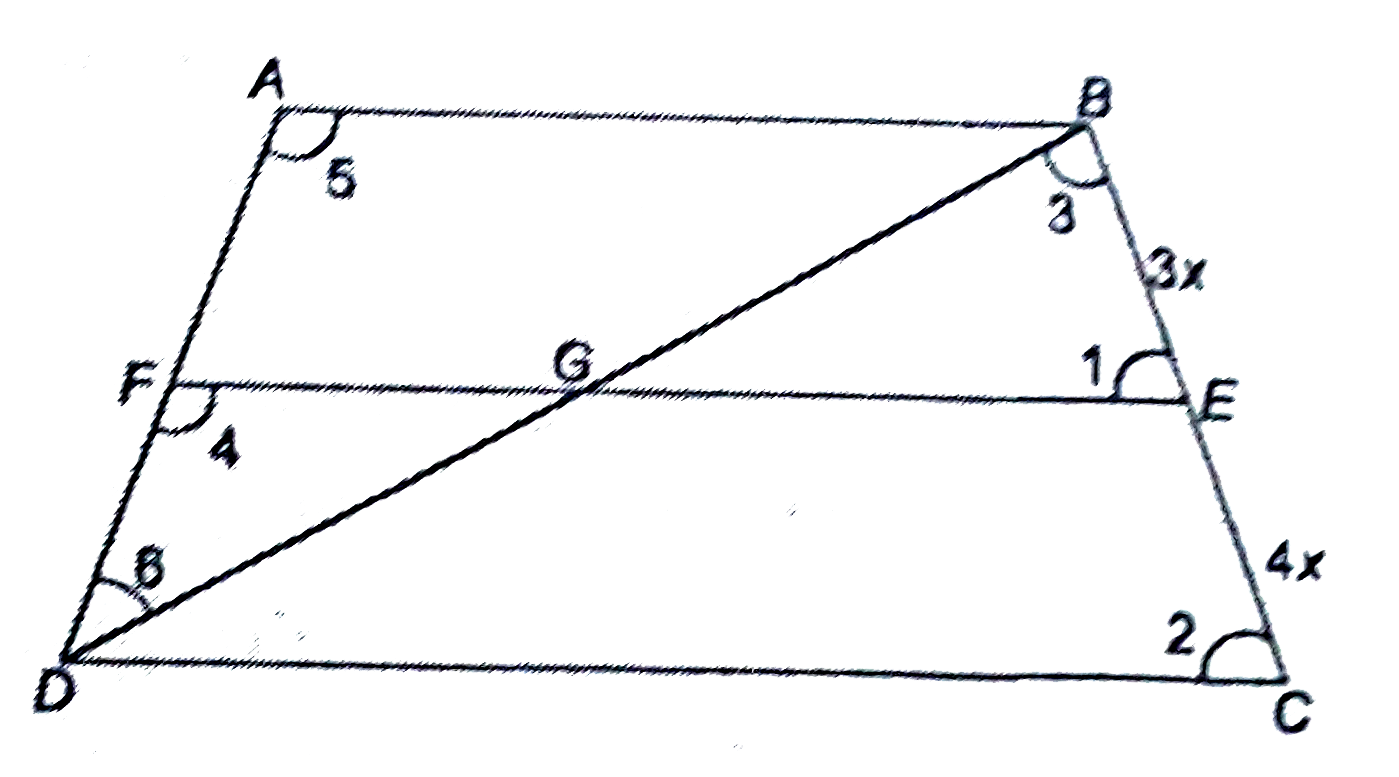
View SolutionIn trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parallel to AB cuts AD in F and BC in E such that BEEC=34 .
Diagonal DB intersects EF at G. prove that &EF= 10AB.
View Solution
