Dry air was passed successively through a solution of 5 g of a solutte in 80 g of water and then through pure water. The loss in mass of solution was 2.5 g and that of pure solvent was 0.04 g The molecular mass of the solute is :
70.31
3.125
312.5
none of these
The correct Answer is:A
To solve the problem, we need to find the molecular mass of the solute based on the given data. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Given Data
- Mass of solute (W_solute) = 5 g
- Mass of solvent (W_solvent) = 80 g
- Loss in mass of solution (ΔW_solution) = 2.5 g
- Loss in mass of pure solvent (ΔW_solvent) = 0.04 g
Step 2: Understand the Concept of Vapor Pressure Lowering
The vapor pressure lowering can be described by the formula:
P0−PsP0=xsolute
Where:
- P0 = vapor pressure of pure solvent
- Ps = vapor pressure of the solution
- xsolute = mole fraction of the solute
Step 3: Relate Loss of Mass to Mole Fraction
The loss in mass of the solution is proportional to the vapor pressure lowering, and the loss in mass of pure solvent is proportional to the vapor pressure of the solvent.
From the problem:
P0−PsPs=ΔWsolventΔWsolution
Substituting the values:
0.042.5
Step 4: Calculate the Ratio
Calculating the ratio:
0.042.5=0.016
Step 5: Set Up the Mole Fraction Equation
Using the mole fraction definition:
nsolutensolute+nsolvent=0.016
Where:
- nsolute=WsoluteMsolute
- nsolvent=WsolventMsolvent
Given that the molar mass of water (solvent) is 18 g/mol, we can express nsolvent:
nsolvent=8018
Step 6: Substitute into the Mole Fraction Equation
Substituting nsolute and nsolvent into the equation:
5Msolute5Msolute+8018=0.016
Step 7: Cross Multiply and Solve for M_solute
Cross multiplying gives:
5Msolute=0.016(5Msolute+8018)
Expanding and simplifying:
5=0.016⋅5+0.016⋅8018Msolute
5=0.08+1.28Msolute
Rearranging gives:
5−0.08=1.28Msolute
4.92=1.28Msolute
Thus:
Msolute=1.284.92
Calculating gives:
Msolute≈0.260g/mol
Final Answer
The molecular mass of the solute is approximately 0.260 g/mol.
- Mass of solute (W_solute) = 5 g
- Mass of solvent (W_solvent) = 80 g
- Loss in mass of solution (ΔW_solution) = 2.5 g
- Loss in mass of pure solvent (ΔW_solvent) = 0.04 g
The vapor pressure lowering can be described by the formula:
P0−PsP0=xsolute
Where:
- P0 = vapor pressure of pure solvent
- Ps = vapor pressure of the solution
- xsolute = mole fraction of the solute
The loss in mass of the solution is proportional to the vapor pressure lowering, and the loss in mass of pure solvent is proportional to the vapor pressure of the solvent.
P0−PsPs=ΔWsolventΔWsolution
Substituting the values:
0.042.5
Calculating the ratio:
0.042.5=0.016
Using the mole fraction definition:
nsolutensolute+nsolvent=0.016
Where:
- nsolute=WsoluteMsolute
- nsolvent=WsolventMsolvent
nsolvent=8018
Substituting nsolute and nsolvent into the equation:
5Msolute5Msolute+8018=0.016
Cross multiplying gives:
5Msolute=0.016(5Msolute+8018)
Expanding and simplifying:
5=0.016⋅5+0.016⋅8018Msolute
5=0.08+1.28Msolute
Rearranging gives:
5−0.08=1.28Msolute
4.92=1.28Msolute
Thus:
Msolute=1.284.92
Calculating gives:
Msolute≈0.260g/mol
The molecular mass of the solute is approximately 0.260 g/mol.
Similar Questions
Dry air was successively passed through a solution of 5g solute in 80g water and then through pure water. The loss in weight of solution was 2.5g and that of pure water was 0.04g. What is mol. wt. of solute ?
View SolutionDry air was suvvessively passed through a solution of 5g solute in 80g water and then through pure water. The loss in weight of solution was 2.5g and that of pure water was 0.04g. What is mol.wt. of solute?
View Solution
Knowledge Check
- Question 1 - Select One
Dry air was passed successively through a solution of 5g of a solute in 180g water and then through pure water. The loss in weight of solutionwas 250g and that of pure solvent 0.04g . The molecular weight of the solute is
A31.25B3.125C312.5DNone of these - Question 2 - Select One
Dry air was passed successively through solution of 5g of a solute in 180g of water and then through pure water. The loss in weight of solution was 2.50g and that of pure solvent 0.04g. The molecualr weight of the solute is:
A(a) 31.25B(b) 3.125C(c ) 312.5D(d) None of these - Question 3 - Select One
Dry air was passed successively through a solution of 5 gm of a solute in 80 gm of water and then through pure ware. The loss in weight of solution was 2.50 gm and that of pure solvent 0.04 gm. What is the molecular weight of the solute
A70.31B7.143C714.3D80
Dry air was passed through a solution containing 20g of a substance in 100-0g of water and then through pure water. The loss in mass of the solution was 2.945g and that of pure water was 0.059g. Calculate the molar mass of the substance.
View SolutionDry air was passed successively through a solution of 5g of a solute in 180g of water and then through pure water and then through pure water. The loss in weight of solution was 2.5g and that of pure solvent 0.04g. The molecular weight of the solute is:
View SolutionDry air is passed through a solution containing 10 g of the solute in 90 g of water and then through pure water. The loss in weight of solution is 2.5 g and that of pure solvent is 0.05 g. Calculate the molecular weight of the solute.
View SolutionLowering in vapour pressure is determined by Ostwald and Walker dynamic methed. It is based on the prinicipal , that when air is allowed to pass through a solvent or solution, it takes up solventvapour with it to get itself saturated at that temperature
I and II are weighted separately before and after passing dry air. Loss in mass of each set, gives the lowing of vapour pressure. The temperature of air, the solution and the solvent is kept constant.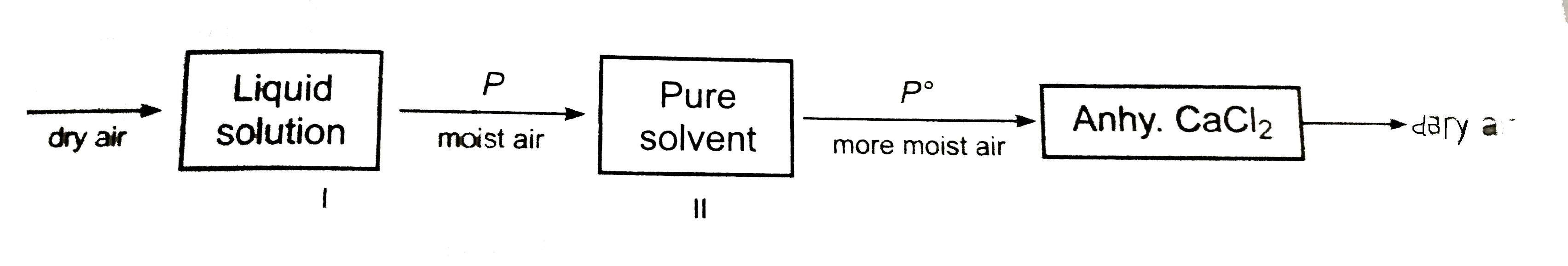
Dry air was passed thorough 9.24 g of solute in 108 g of water and then through pure water. The loss in mass of solution was 3.2 g and that of pure water 0.08 g . The molecular mass (g/mol) of solute is nearly :View SolutionLowering of vapour pressure is determined by Ostward and Walner dynamic method. It is based on the principle, when air is allowed to pass through a solvent or solution, it takes up solvent vapour with it to get itself saturated with vapours at that temperature.
dry ari → solution PA−−→solventAP+A−−→Anhy.CaCl2→ air.
A and B are weighted separately before and after passing dry air. Loss in weight of each set, gives the lowering of vapour pressure. The temperature of air, the solution and the solvent is kept constant.
Dry air was passed through 5 g of solute iini 80 g of water and then through pure water. The loss in weight of solution was 2.5 g and that of pure water was 0.04 g. The molecule weight of solute is:View Solution

