What are the dimensions of χ, the magnetic susceptibility? Consider an H-atom. Guess an expression for χ upto a constant by constructing a quantity of dimensions of χ, out of parameters of the atom: e, m, v, R and μ0. Here, m is the electronic mass, v is electronic velocity, R is Bohr radius. Estimate the number so obtained and compare with the value of ∣∣χ⌈10−5 for any solid material.
AS I and H both have same units and dimensions , hence X has no dimensions. Here, in this question, X is to be related with e,m,v,R and μ0 . We know that dimensions of μ0=[M<hη−1]
From Biot-Savart's law,
dB=μ04πIdtsinθr2
⇒μ0=4πr2dBIdlsinθ=4πr2ldlsinθ×fqvsinθ [∵dB=Fqvsinθ]
∴ Dimensions of μ0=L2×(MLT−2)(QT−1)(L)×1×(Q)(LT−1)×(1)=[MLQ−2]
Where Q is the dimension of charge.
As X dimensionless it should have no involvement of change Q in its dimensional formula it will be so if μ0. and e togther should have the value μ0θ2. as has the dimensions of charge
Let X=μ0θ2mavbRc ........(i)
Where a,b,c are the power of m,v and R respectively, such that relation (i) is statisfied
Dimensional equation of i is.
[M0L0T0Q0]=[MLQ−2]xx[Q2][Ma]×(LT−1)b×[L]c
=[M1+a+L1+b+cT−bQ0]
Equating the powers of M L and T, we get
0=1+a⇒a=−1,0=1+b+c
=0=−0⇒0,0=1+0+corc=−1
Putting values in Eq. (i) we get
X=μ2e2m−1v2R−1=μ0θ2mR
Here, μ0=4π×10−7TmA−1
e=1.6×10−19C
m=9.1×10−31kg,R=10−10m
X=(4π×10−7)×(1.6×10−19)2(9.1×10−31)×10−10=10−4
∴xXgiven solid=10−410−5=10
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Electrostatic Potential And Capacitance33videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - NCERT EXEMPLARCHAPTER - MOVING CHARNGES AND MAGNETISMEXERCISE - Moving Charnges And Magnetism29videos
MOVING CHARNGES AND MAGNETISM
Similar Questions
Classically, an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size? Why is an atom not, say, thousand times bigger than its typical size? The question had greatly puzzled Bohr before he arrived at his famous model of the atom that you have learnt in the text. To simulate what he might well have done before his discovery, let us play as follows with the basic constants of nature and see if we can get a quantity with the dimensions of length that is roughly equal to the known size of an atom (~10–10m).
(a) Construct a quantity with the dimensions of length from the fundamental constants e, me, and c. Determine its numerical value.
(b) You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non-relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for ‘something else’ to get the right atomic size. Now, the Planck’s constant h had already made its appearance elsewhere. Bohr’s great insight lay in recognising that h, me, and e will yield the right atomic size. Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.View SolutionClassically, an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size? Why is an atom not, say, thousand times bigger than its typical size? The question had greatly puzzled Bohr before he arrived at his famous model of the atom that you have learnt in the text. To simulate what he might well have done before his discovery, let us play as follows with the basic constants of nature and see if we can get a quantity with the dimensions of length that is roughly equal to the known size of an atom (~10–10m).
(a) Construct a quantity with the dimensions of length from the fundamental constants e, me, and c. Determine its numerical value.
(b) You will find that the length obtained in (a) is many orders of magnitude smaller than the atomic dimensions. Further, it involves c. But energies of atoms are mostly in non-relativistic domain where c is not expected to play any role. This is what may have suggested Bohr to discard c and look for ‘something else’ to get the right atomic size. Now, the Planck’s constant h had already made its appearance elsewhere. Bohr’s great insight lay in recognising that h, me, and e will yield the right atomic size. Construct a quantity with the dimension of length from h, me, and e and confirm that its numerical value has indeed the correct order of magnitude.View Solution
Knowledge Check
- Question 1 - Select One
The wave function ψn,l,m is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n,l and m. Here r is distance from nucleus θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.

For He+ ion the only Incorrect combination isA(II)(ii)(Q)B(I)(i)(S)C(I)(i)(R)D(I)(iii)(R) - Question 2 - Select One
In an ordianary atom, as a first approximation, the motion of the nucleus can be ignored. In a positronium atom a positronreplaces the proton of hydrogen atom. The electron and positron masses are equal and , therefore , the motion of the positron cannot be ignored. One must consider the motion of both electron and positron about their center of mass. A detailed analyasis shows that formulae of Bohr's model apply to positronium atom provided that we replace me by what is known reduced mass is me/2.
If the Rydberg constant for hydrogen atom is R , then the Rydberg constant for positronium atom isA2RBRCR/2D4R - Question 3 - Select One
The wave function, ψn,l,ml is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterised by the quantum number n,l and ml. Here r is distance from nucleus, θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.
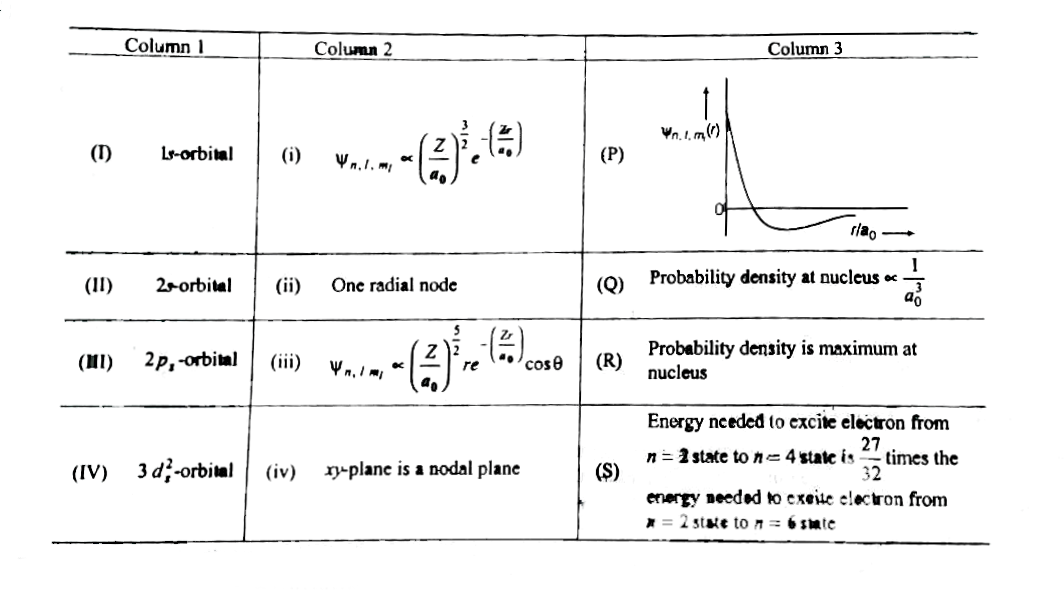
For hydrogen atom, the only CORRECT combination isA(I ) (i)(P)B(I)(iv)(R)C(II)(i)(Q)D(I)(i)(S)
The Betatron was the first important machine for producing high energy electrons. The action of the betatron depends on the same fundamental principle as that of the transformer in which an alternating current applied to a primary coil induces an altermating current usually with higher or lower voltage in the secondary coil. In the betatron secondary coil is replaced by a doughnut shaped vacuum chamber.Electron produced in the doughnut from a hot filament, are given a preliminary acceleration by the application of an electric field having potential difference of 20kV to 70kV, when an alternating magnetic field is applied parallel to the axis of the tube, two effects are produced (1) an electromotive force is produced in the electron orbit by the changing magnetic flux that gives an additional energy to the electrons (2) a radial force is produced by the action of magnetic field whose direction is perpendicular to the electron velocity. Which keeps the electron moving in a circular path. Conditions are arranged such that the increasing magnetic field keeps the electron in a circular orbit of constant radius. The mathematical relation between the betatron parameters to ensure the above condition is called BETATRON condition.
If the orbit radius of the circular path traced by the electron is R, magnetic field is B, speed of the electron is v, mass of the electron is m, charge on the electron is e and ϕ is the flux within the orbit of radius R. Then answer the following questions based on the above comprehension.
What is the value of d(m|→v|)dt ?View SolutionUsing Rautherfold model of the atom, derive the expression for the total electron in hydrogen atom. What is the significance of total negative energy possedssed by the electron?
Using Bohr's postulates of the atomic model, derive the expression for radius of nth electron orbit. Hence obtain the expression for Bohr's radius
This therory developed is applicable to Hydrogen atoms and ions having just one electron. Let us assume that the nucleus has a positive charge Ze (i.e. ther are Z protons in it) and electrons moves with a consant speed V along a circle of radius r with the centre at nucleus By Coulomb's lawView SolutionThe wave function Φn,l,m1 is a methematical function whose value depends upon shperical upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers, n,l and m1. Here r is distance from nucleus, θ is colatitude and ϕ is azimuth. in the mathematical functions given in the table, Z is atomic number, a0 is Bohr radius.
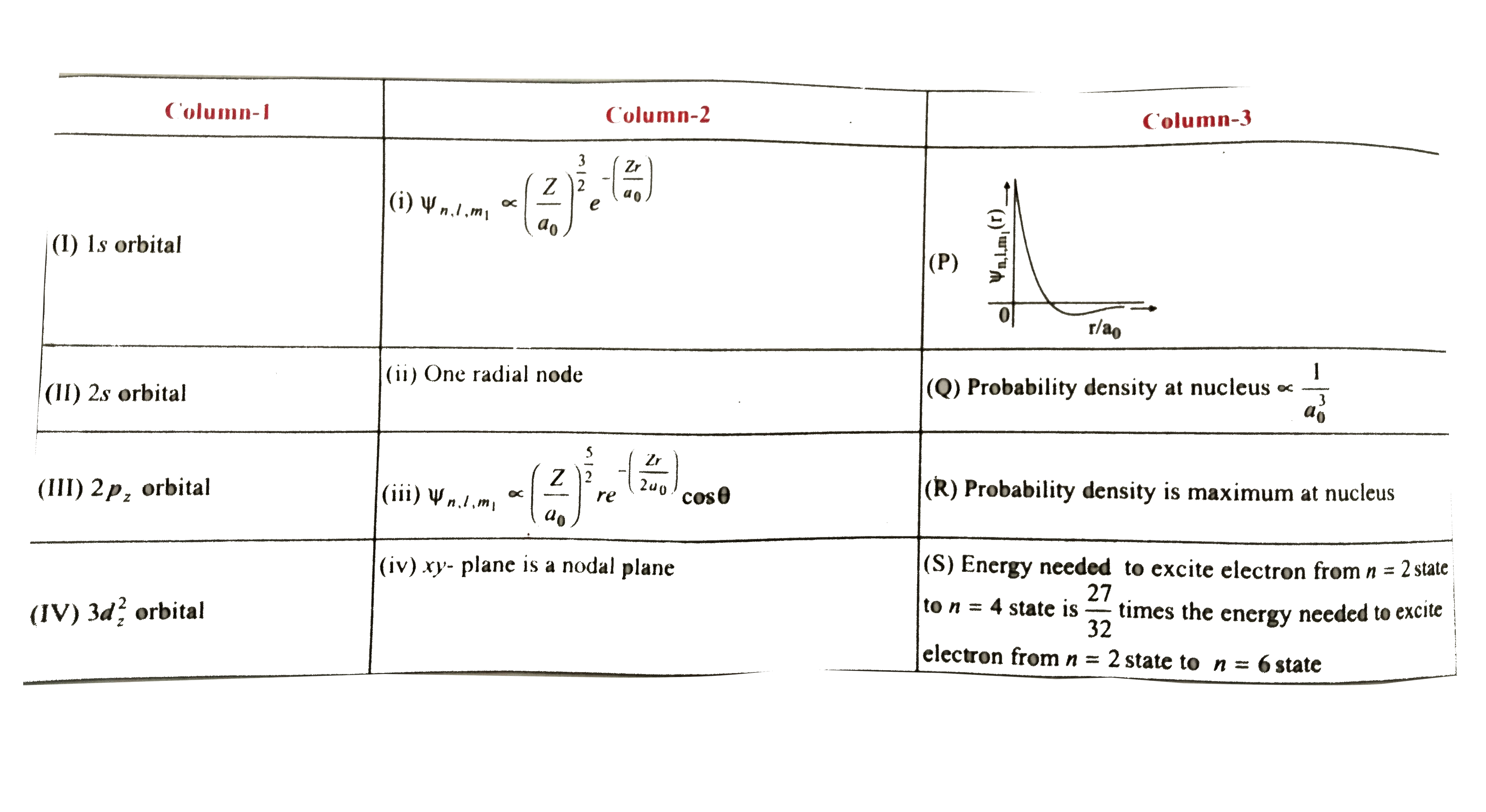 .
.
Q. For hydrogen atom the only CORRECT combination is :View SolutionThe wave function ψn,l,m is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterized by the quantum numbers n,l and m. Here r is distance from nucleus θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.
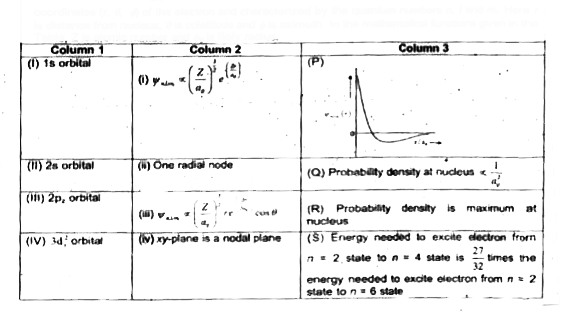
For hydrogen atom, the only correct combination isView SolutionThe wave function, ψn,l,ml is a mathematical function whose value depends upon spherical polar coordinates (r,θ,ϕ) of the electron and characterised by the quantum number n,l and ml. Here r is distance from nucleus, θ is colatitude and ϕ is azimuth. In the mathematical functions given in the Table, Z is atomic number and a0 is Bohr radius.
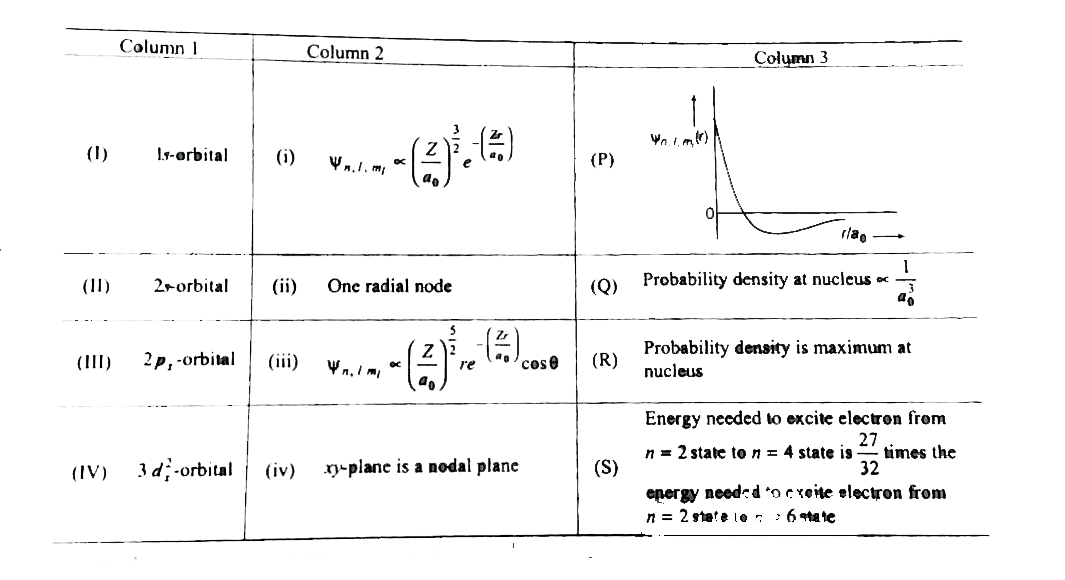
For the given orbital in Column I, the Only CORRECT combination for any hydrogen-like species isView Solution

