For an LCR circuit driven at frequency ω, the equation reads Ldidt+Ri+qC=υi=υmsinωt
(i) Multiply the equation by I and simplify where possible. (ii) Interpret each term physically.
(iii) Cast the equation in the form of a conservation of energy statement.
(iv) Intergrate the equation over one cycle to find that the phase difference between υ and i must be acute.
Video Solution
Text Solution
The correct Answer is:A
Consider the L-C-R circuit. Applying KVL for the loop, we can write.
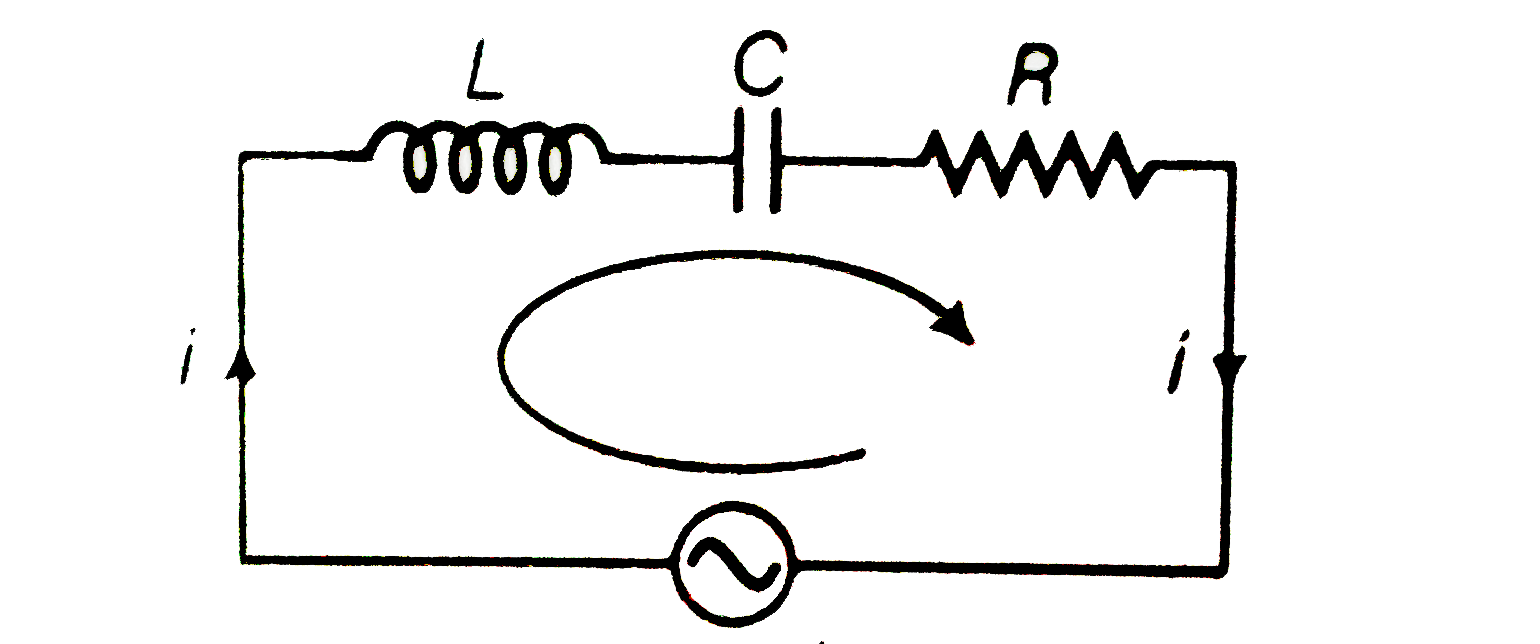
⇒Ldidt+qC+iR=Vmsinωt……….(i)
Multiplying both sides by i, we get
Lididt+qCi+i2R=(Vmi)sinωt=Vi............(ii)
where Lididt=ddt(12Li2) = rate of change of energy stored in an inductor.
Ri2= joule heating loss
qCi=ddt(q22C)= rate of change of energy stored in the capacitor.
Vi= rate at which driving force pours in energy. It goes into (i) ohmic loss and ii) increase of stored energy.
Hence, Eq. (i) is in the form of conservation of energy statement. Integrating both sides of Eq. (ii) with respect to time over one full cycle (0→T) we may write.
∫t0ddt(12Li2+q22C) dt + ∫T0Ri2dt=∫T0V
⇒0+(+ve)=∫T0V
⇒∫T0dt>0 if phase difference between V and i is a constant and acute angle.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The equations of two SH M's are
X1=4sin(ωt+π/2).X2=3sin(ωt+π)A6 unitsB5 unitsC1 unitsD7 unitsIf i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
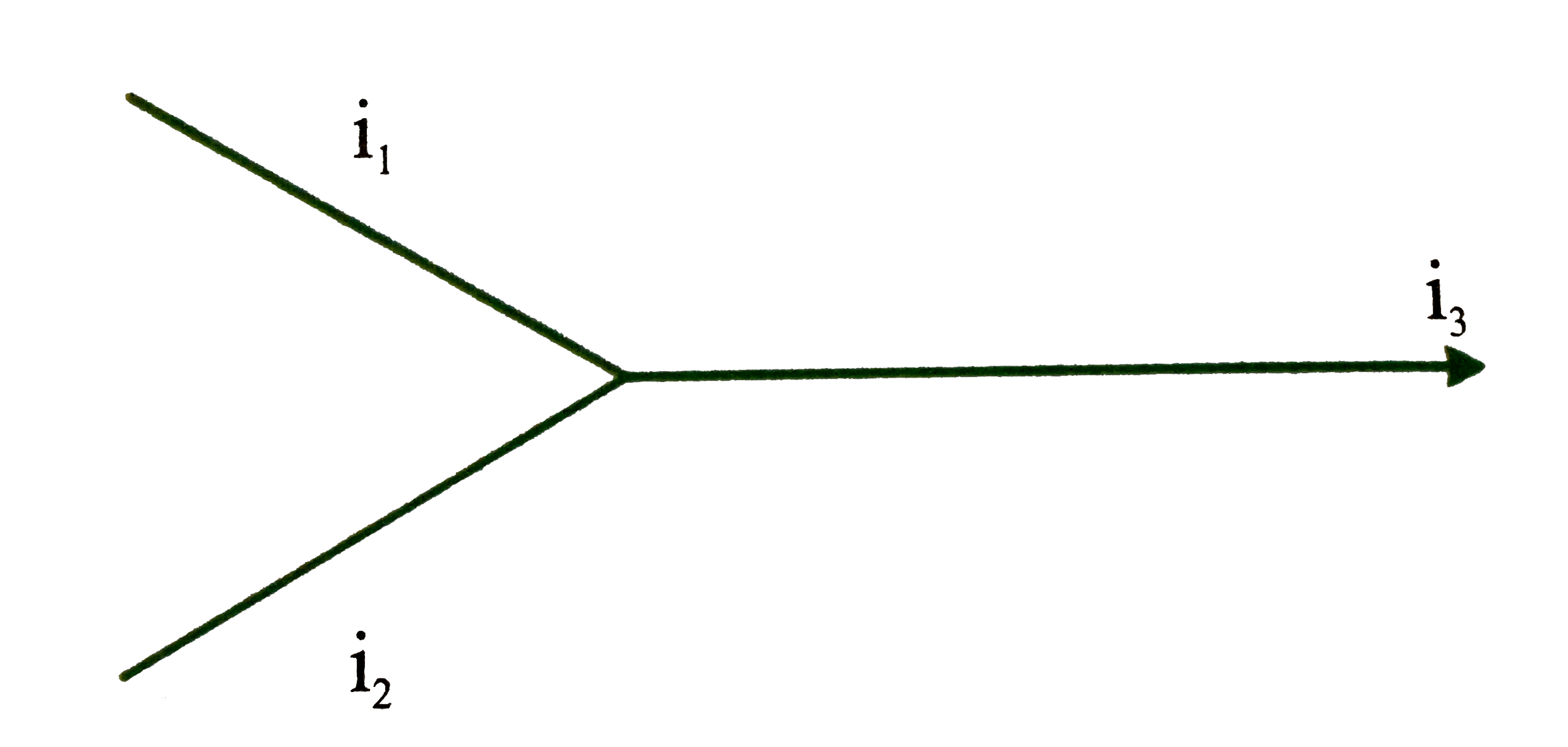 A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]
A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]The displacement of a particle is represented by the equation y=sin2ωt the motion is
Anon - periodicBperiodic but not simple harmonicCsimple harmonic with period 2π/ωDsimple harmonic with period π/ω
The equation of an alternating current is I=20sin300 pi t .Calculate the frequency and r.m.s value of current
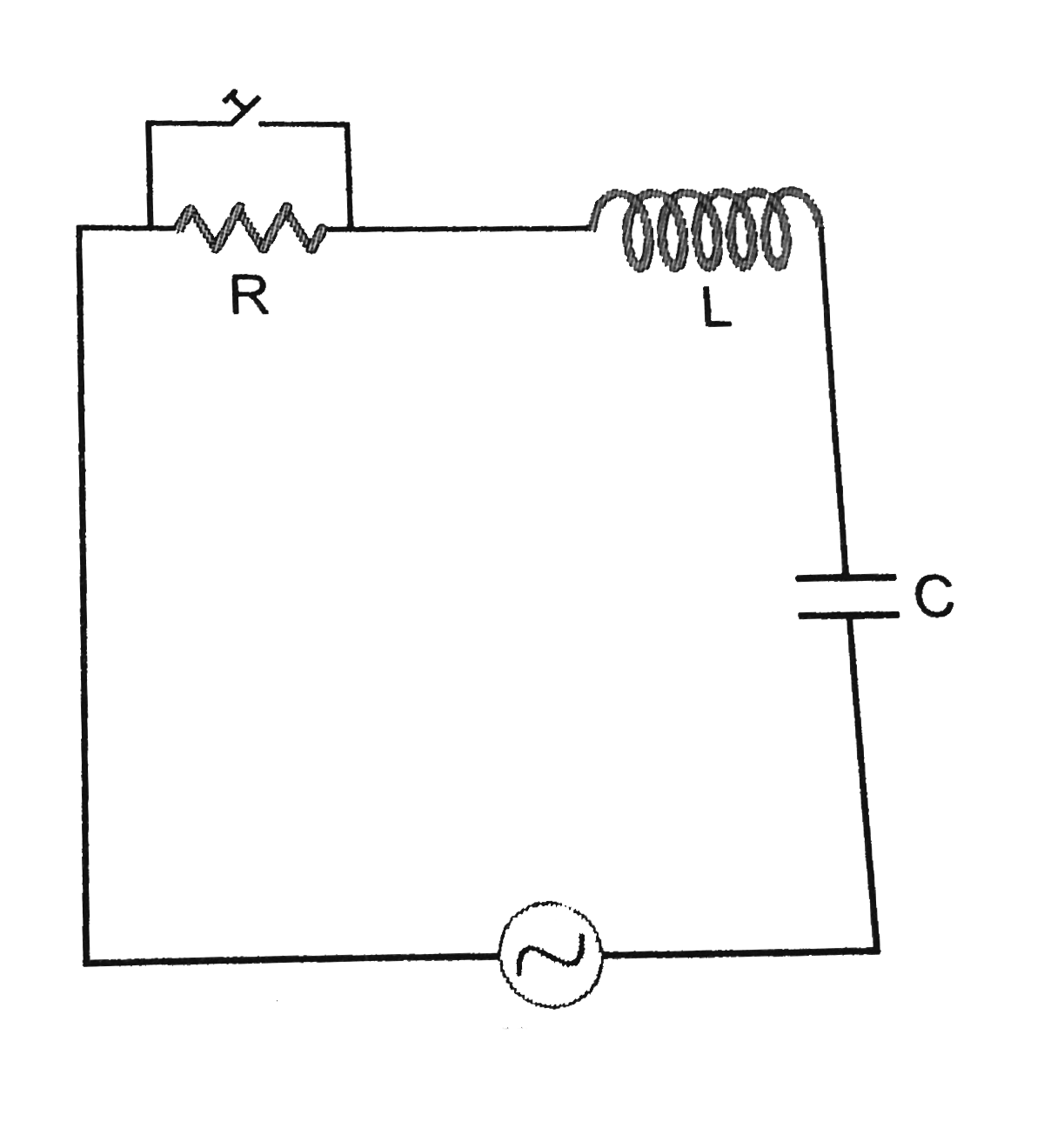
View SolutionIn the LCR circuit shown in Fig., the ac driving voltage is υ=υmsinωt.
(i) Write down the equation of motion for q (t).
(ii) At t=t0, the source stops and R is short circuited.
Now write down how much energy is stored in each of L and C.
(iii) Describe subsequent motion of charges.
View SolutionIn terms of q, the voltage equation for series L-C-R circuit is given by
View SolutionFor an ac circuit V=15sinωt and I=20cosωt the average power consumed in this circuit is
View Solutiony=Acosωt+Bsinωt is a solution of the differential equation
View Solution
