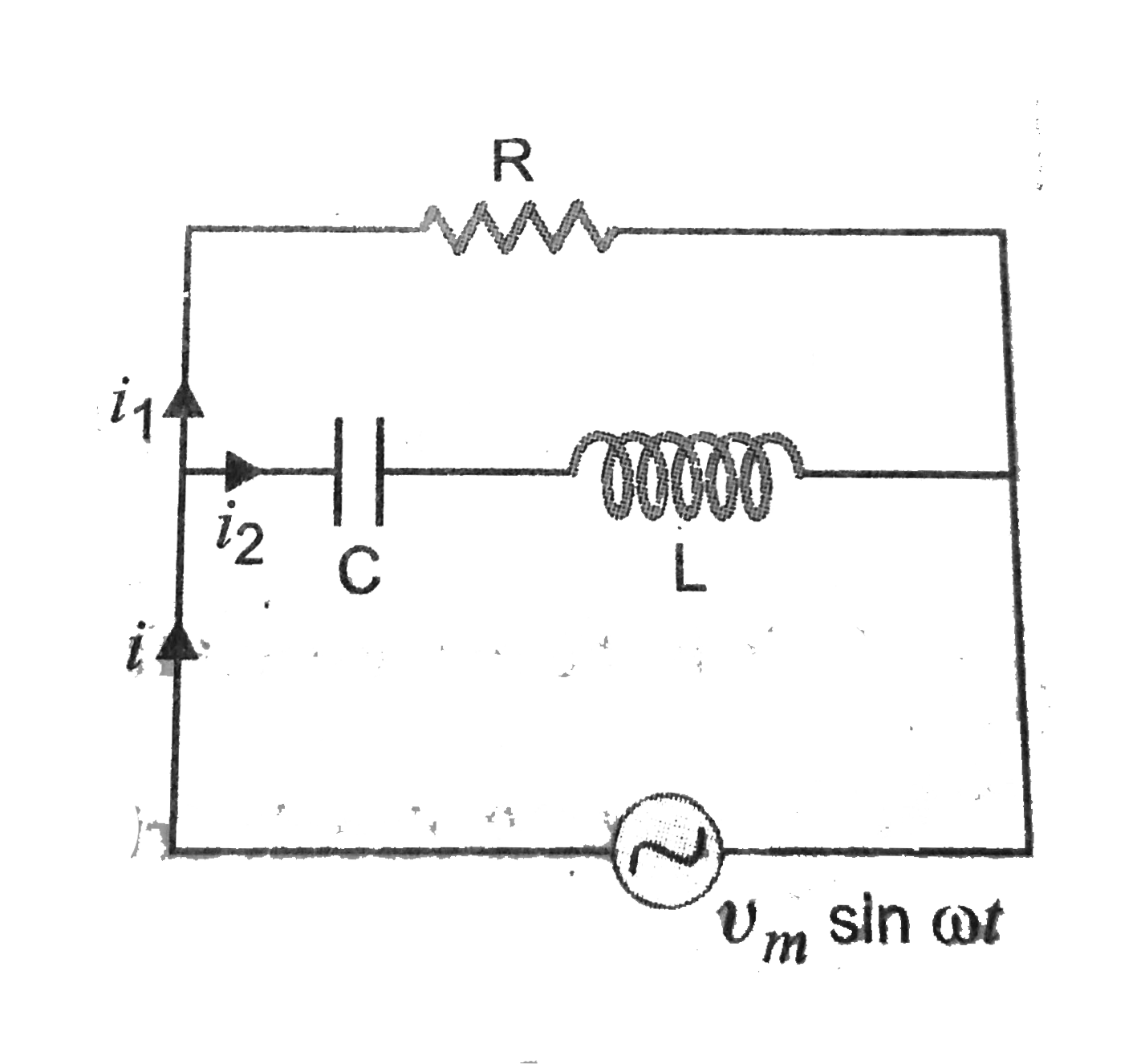
Consider the L-C-R circuit shown in the fiure. Find the net current I and the phase of i. Show that $i = \frac{V}{Z}$ . Find the impedance Z of this circuit.

Text Solution

Verified by Experts

The correct Answer is:A

In the given figure $i$ is the total current from the source. It is divided into two parts, $i_{1}$ through R and $i_{2}$ throgh series combination of C and L.
So, we can write $i = i_{1} + i_{2}$
$V_{m} sin ω t = R i_{1}$ (from the circuit diagram)
$i_{1} = \frac{V_{m} sin ω t}{R}$ .............(i)
If $q_{2}$ is charge on the capacitor at any time t, then for series combination of C and L.
Applying KVL inthe Lower circuit as shown.

$\frac{q_{2}}{C} + \frac{L d i_{2}}{d t} - V_{m} sin ω t = 0$
$\Rightarrow \frac{q_{2}}{C} + \frac{L d_{2} q_{2}}{{(d t)}^{2}} = V_{m} sin ω t$ $[∴ i_{2} = \frac{d q_{2}}{d t}]$ ......(ii)
Let $q_{2} = q_{m} sin (ω t + ϕ)$ ..............(iii)
$\frac{d q_{2}}{d t} = q_{m} cos (ω t + ϕ)$
$\Rightarrow \frac{d^{2} q_{2}}{{d t}^{2}} = - q_{m} ω^{2} sin (ω t + ϕ)$
Now putting the values in Eq. (ii), we get
$q_{m} [\frac{1}{C} + l (- ω^{2})] sin (ω t + ϕ) = V_{m} sin ω t$
If $ϕ = 0$ and $(\frac{1}{C} - L ω 6 (2)) > 0,$
then $q_{m} = \frac{v_{m}}{\frac{1}{C} - L ω^{2}}$ ..............(iv)
From Eq. (iii), $i_{2} = \frac{d q_{2}}{d t} = ω q_{m} cos (ω t + ϕ)$
Using Eq. (iv), $i_{2} = \frac{ω V_{m} cos (ω t + ϕ)}{\frac{1}{C} - L ω^{2}}$
Taking $ϕ = 0, i_{2} = \frac{V_{m} cos (ω t)}{\frac{1}{ω C} - L ω}$
From Eqs. (i) and (v), we find that $i_{1}$ and $i_{2}$ are out of phase by $\frac{ϕ}{2}$
Now, $i_{1} + i_{2} = \frac{V_{m} sin ω t}{R} + \frac{V_{m} cos ω t}{\frac{1}{ω C} - L ω}$
Put $\frac{V_{m}}{R} = A = C cos ϕ$ and $\frac{V_{m}}{\frac{1}{ω C} - L ω} = B = C sin ϕ$
$∴ i_{1} + i_{2} = C cos ϕ sin ω t + C sin ϕ cos ω t$
$= C = \sqrt{A^{2} + B^{2}}$
and $ϕ = \frac{{tan}^{- 1} B}{A} C = {⎡ ⎣ \frac{V_{m}^{2}}{R^{2}} + \frac{V_{m}^{2}}{\frac{1}{ω C} - L ω} ⎤ ⎦}^{1 / 2}$
and $ϕ = {tan}^{- 1} = \frac{R}{\frac{1}{ω C} - L ω}$
Hence, $i = i_{1} + i_{2} = {⎡ ⎢ ⎢ ⎢ ⎣ \frac{V_{m}^{2}}{R^{2}} + \frac{V_{m}^{2}}{{(\frac{1}{ω C} - L ω)}^{2}} ⎤ ⎥ ⎥ ⎥ ⎦}^{1 / 2} sin (ω t + ϕ)$
or $\frac{i}{V_{m}} = \frac{1}{Z} = {⎡ ⎢ ⎢ ⎢ ⎣ \frac{1}{R^{2}} + \frac{1}{{(\frac{1}{ω C} - L ω)}^{2}} ⎤ ⎥ ⎥ ⎥ ⎦}^{1 / 2}$
This is the expression for impedance Z of the circuit.

Updated on:21/07/2023

|

Class 12 PHYSICS ALTERNATING CURRENT

Topper's Solved these Questions

ATOMSBOOK - NCERT EXEMPLARCHAPTER - ATOMSEXERCISE - Atoms
29 Videos

Similar Questions

Knowledge Check

Find the current $I$ in circuit

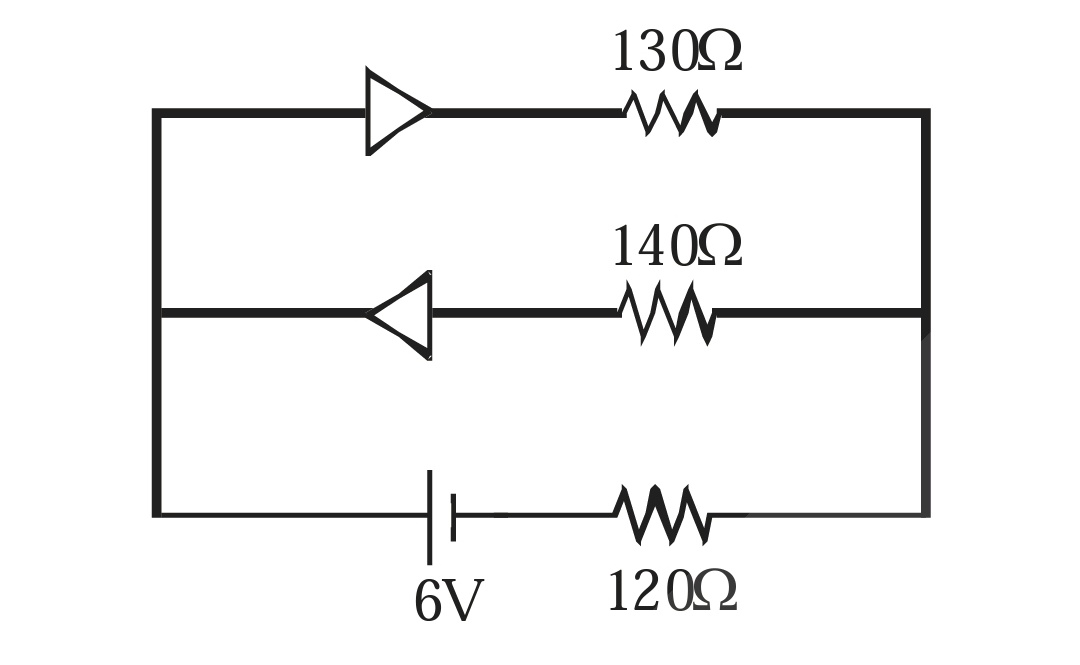A20 mA
B2 mA
C0.1 mA
D10 mA
Find the current I in the given circuit

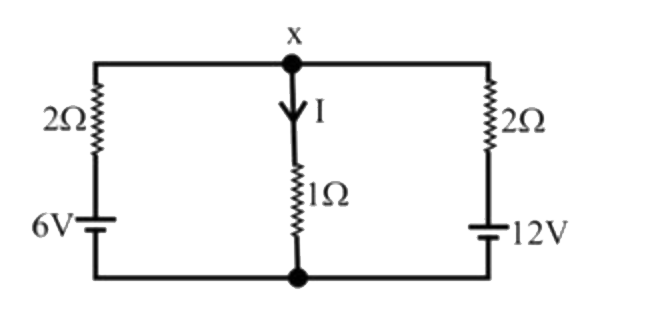A $2 A$
B4. 5 A
C $6 A$
D1.5 A
Find current (i) in circuit shown in figure.

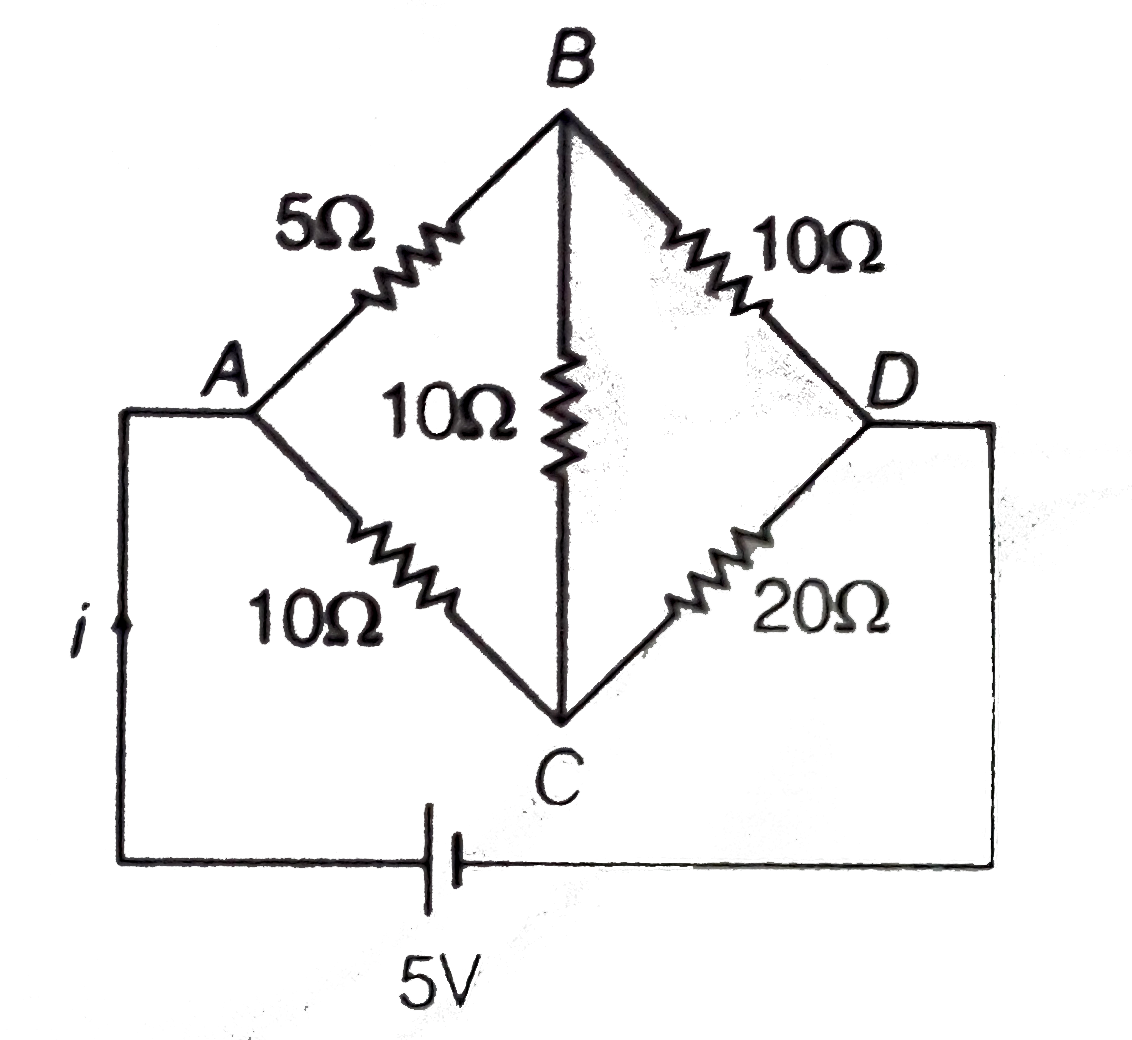A0.5 A
B0.2 A
C0.041666666666667
D0.083333333333333

NCERT EXEMPLAR-ALTERNATING CURRENT-Alternating Current

Home
Ask Doubt
Profile