If three mutually perpendicular lines have direction cosines (l1,m1,n1),(l2,m2,n2)and(L3,m3,n3), then the line having direction cosines l1+l2+l3,m1+m2+m3,andn1+n2+n3, make an angle of
→a=l1ˆi+m1ˆj+n1wˆk
→b=l2ˆi+m2ˆj+n2wˆk
→c=l3ˆi+m3ˆj+n3wˆk
the direction vector associated with directions cosines I1+I2+I3,m1+m2+m3,n1+n2+n3
→p=(11+l2+l3)ˆi+(m1+m2+m3)ˆi+(n1+n2+n3)wˆk
As, lines associated with direction vectors a, b and c are mutually perpendicular
We have →a⋅→b=0.....
⇒I1I2+m1m2+n1n2=0
Similarly, →a⋅→c=0
⇒I1I3+m1m3+n1n3=0
→b⋅→c=0
⇒I2I3+m2m3+n2n3=0
x,y,z be the angles made by direction vectors a, b and c respectively with p
Therefore, cosx=→a⋅→p
⇒cosx=l1(l1+I2+I3)+m1(m1+m2+m3)+n1(n1+n2+n3)
⇒cosx=l21+l1l2+l1l3+m21+m1m2+m1m3+n21+n1n2+n1n3
⇒cosx=l21+m21+n21+(l1l2+m1m2+n1n2)+(l1l3+m1m3+n1n3)
l21+m21+n21=1 because sum of squares of direction cosines of a line is equal to 1
⇒cosx=1+0=1......
[ From, 1 and 2]
cosy=1andcosz=1
⇒x=y=z=0
So angle made by vector p, with vectors a, b and c are equal!
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two lines with direction cosines l1,m1,n1andl2,m2,n2 are at right angle of
Al1l2−m1m2−n1n2=0Bl1l2+m1m2+n1n2=0Cl2=l2,m1=m2,n1=n2Dl1l2=m1m2=n1n2l = m = n = 1 are the direction Cosines of
AX-axisBY-axisCZ-axisDno lineThe direction cosines of a line equally inclined to three mutually perpendiclar lines having direction cosines as l1,m1,n1,l2,m2,n2 and l3,m3,n3 are
Al1+l2+l3,m1+m2+m3,n1+n2+n3Bl1+l2+l3√3,m1+m2+m3√3,n1+n2+n3√3Cl1+l2+l33,m1+m2+m33,n1+n2+n33Dnone of these
If the direction cosines of two lines are l1,m1,n1 and l2,m2,n2, then find the direction cosine of a line perpendicular to these lines.
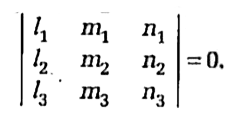
View SolutionProve that the three lines from O with direction cosines l1,m1,n1:l2,m2,n2:l3,m3,n3 are coplanar, if l1(m2n3−n2m3)+m1(n2l3−l2n3)+n1(l2m3−l3m2)=0
View SolutionStatement 1: The direction cosines of one of the angular bisectors of two intersecting line having direction cosines as l1,m1,n1andl2,m2,n2 are proportional to l1+l2,m1+m2,n1+n2. Statement 2: The angle between the two intersection lines having direction cosines as l1,m1,n1andl2,m2,n2 is given by cosθ=l1l2+m1m2+n1n2.
View SolutionIf θ is the acute angle between two intersecting straight lines, one having direction cosines l1,m1,n1 and the other having direction cosines l2,m2,n2 then sin2θ=
View SolutionIf l,m,n are direction cosines of the line then −l,−m,−n can be
View Solution