If the coordinates of the two points are P(−2,3) and Q(−3,5) , then (Abscissa of P)−(Abscissa of Q) is
−5
1
−1
−2
The correct Answer is:B
To solve the problem, we need to find the difference between the abscissa (x-coordinate) of point P and the abscissa of point Q.
Step 1: Identify the coordinates of points P and Q.
- The coordinates of point P are given as P(-2, 3).
- The coordinates of point Q are given as Q(-3, 5).
Step 2: Identify the abscissa of each point.
- The abscissa of point P (x-coordinate) is -2.
- The abscissa of point Q (x-coordinate) is -3.
Step 3: Calculate the difference between the abscissa of P and the abscissa of Q.
- We need to calculate: (Abscissa of P) - (Abscissa of Q)
- This can be written as: -2 - (-3)
Step 4: Simplify the expression.
- When we subtract a negative number, it is the same as adding its positive counterpart. Therefore:
- -2 - (-3) = -2 + 3
Step 5: Perform the final calculation.
- -2 + 3 = 1
Final Answer:
The difference between the abscissa of P and the abscissa of Q is 1.
---
- The coordinates of point P are given as P(-2, 3).
- The coordinates of point Q are given as Q(-3, 5).
- The abscissa of point P (x-coordinate) is -2.
- The abscissa of point Q (x-coordinate) is -3.
- We need to calculate: (Abscissa of P) - (Abscissa of Q)
- This can be written as: -2 - (-3)
- When we subtract a negative number, it is the same as adding its positive counterpart. Therefore:
- -2 - (-3) = -2 + 3
- -2 + 3 = 1
The difference between the abscissa of P and the abscissa of Q is 1.
Topper's Solved these Questions
Similar Questions
For what value of p the point (p,2) lies on the line 3x+y=11? If the coordinates of two points are P(−2,3)andQ(−3,5), then find (abscissa of P) - (abscissa of Q).
View SolutionIf the coordinates of two points are A(3,4) and B(-2,5), then find the value of (abscissa of A) - (abscissa of B).
View Solution
Knowledge Check
In a cartesian coordinate system, the coordinates of two points P and Q are (2,3,-6) and (-2,-5,7) respectively, the vector ¯¯¯¯¯¯PQ is represented by
A−4ˆi−8ˆj−13ˆkB−4ˆi+8ˆj−13ˆkC4ˆi−8ˆj−13ˆkD−4ˆi−8ˆj+13ˆkIf A(−2,3)andB(−3,5) are two given points then (abscissa of A) - (abscissa of B) = ?
A−2B1C−1D2Find the coordinates of a point lying between the points P(3, -4) and Q(-2, 5) that is twice as far from P as from Q.
A(-7, 14)B(7, -14)C(-1/3, 2)D(1/3, -2)
If the co-ordinate of two points are P ( -3,5) and Q( 4 , -3) (i) Find the value of ( Ordinate of Q – Abscissa of P) (ii) Find the value of (Abscissa of P – Abscissa of Q)
View SolutionThe coordinates of the points P and Q are respectively (4,-3) and (-1,7). Find the abscissa of a point R on the line segment PQ such that PRPQ=35 .
View SolutionIn figure LM is a line parallel to the Y-axis at a distance of 3 units .
(i) What are the coordinates of the points P,R and Q ?
(ii) What is the difference between the abscissa of the points L and M ?
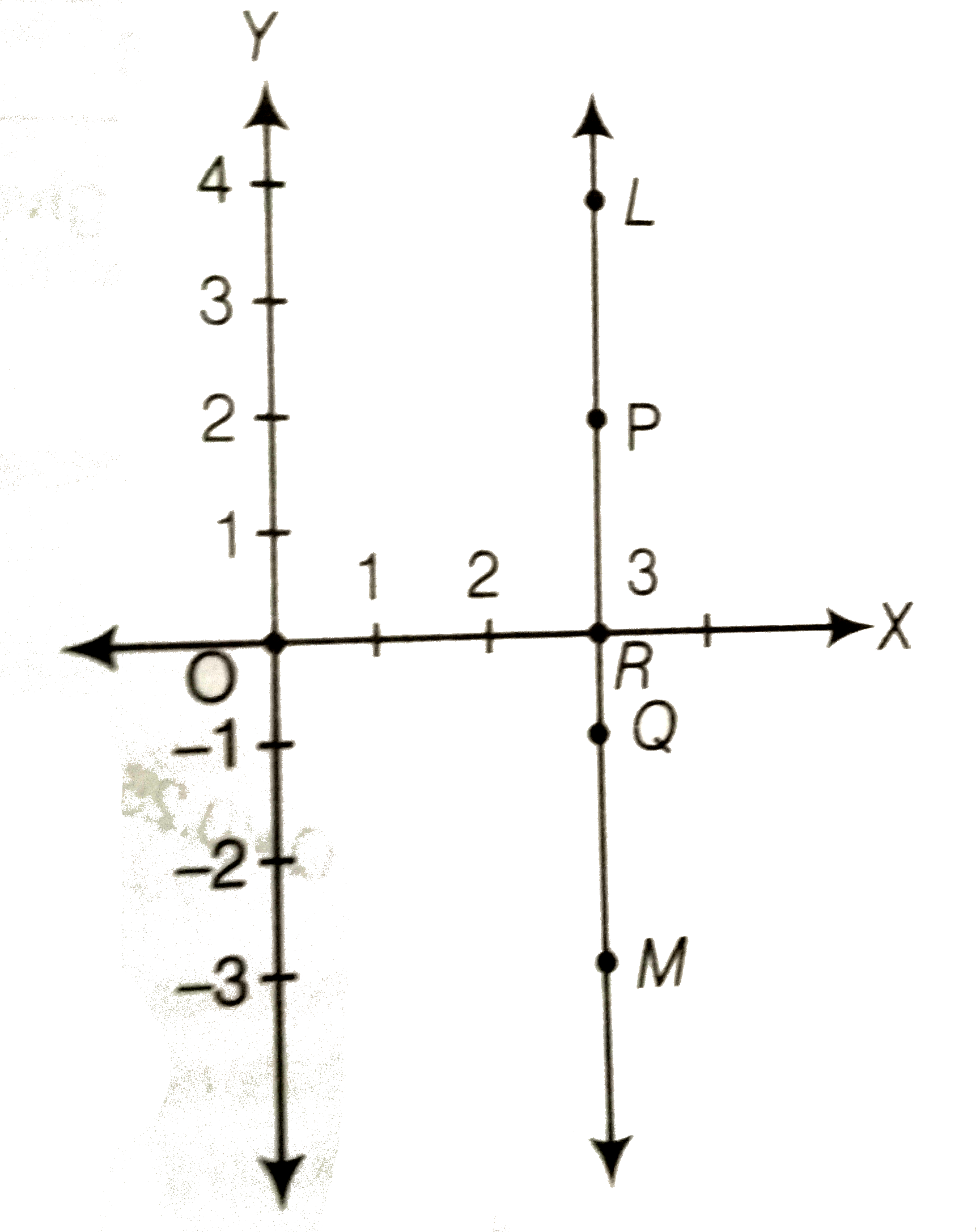
View SolutionIf the coordinates of a point are (-2, 5), then its ordinate is and its abscissa is. _______________
View SolutionThe abscissa of the point (3,5) is
View Solution