A gas mixture consists of molecules of A,B and C with masses $m_{A} > m_{B} > m_{C} .$ Rank the three types of molecules in decreasing order of (a) average KE (b) rms speeds.

Video Solution

Text Solution

Verified by Experts

The average KE will be the same , as conditions of temperature and pressure are the same.
$Now as V_{rms} = \sqrt{\frac{3 p V}{M}} = \sqrt{\frac{3 R T}{M}}$
$= \sqrt{\frac{3 R T}{m N}} = \sqrt{\frac{3 k T}{m}}$
$where m = molar mass of the gas$
m = mass of each molecular of the gas
R = gas constnat
$Clearly V_{rms} \propto \sqrt{\frac{1}{m}}$
(b). As K= Botlzmann constant
T= absolute temperature (same for all)
$But m_{A} > m_{B} > m_{c}$
${(V_{rms})}_{A} < {(V_{rms})}_{B} < {(V_{rms})}_{C}$
$∴ or {(V_{rms})}_{C} > {(V_{rms})}_{B} > {(V_{rms})}_{A}$

|

Updated on:21/07/2023

Class 11 PHYSICS KINETIC THEORY OF GASES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A gas mixture consists of molecules of type 1,2 and 3, with molar masses $m_{1} > m_{2} > m_{3} . V_{r m s} and - K$ are the r.m.s. speed and average kinetic energy of the gases. Which of the following is true-
A ${(V_{r m s})}_{1} < {(V_{r m s})}_{2} < {(V_{r m s})}_{3} & {(¯ ¯¯ ¯ K)}_{1} = {(¯ ¯¯ ¯ K)}_{2} = {(¯ ¯¯ ¯ K)}_{3}$
B ${(V_{r m s})}_{1} = {(V_{r m s})}_{2} = {(V_{r m s})}_{3} & {(¯ ¯¯ ¯ K)}_{1} = {(¯ ¯¯ ¯ K)}_{2} > {(¯ ¯¯ ¯ K)}_{3}$
C ${(V_{r m s})}_{1} > {(V_{r m s})}_{2} > {(V_{r m s})}_{3} & {(¯ ¯¯ ¯ K)}_{1} < {(¯ ¯¯ ¯ K)}_{2} > {(¯ ¯¯ ¯ K)}_{3}$
D ${(V_{r m s})}_{1} > {(V_{r m s})}_{2} > {(V_{r m s})}_{3} & {(¯ ¯¯ ¯ K)}_{1} < {(¯ ¯¯ ¯ K)}_{2} < {(¯ ¯¯ ¯ K)}_{3}$
Question 2 - Select One
Rank the hydrogen atoms $(H_{a}, H_{b}, H_{c})$ present in the following molecule is decreasing order of their acidic strengh.

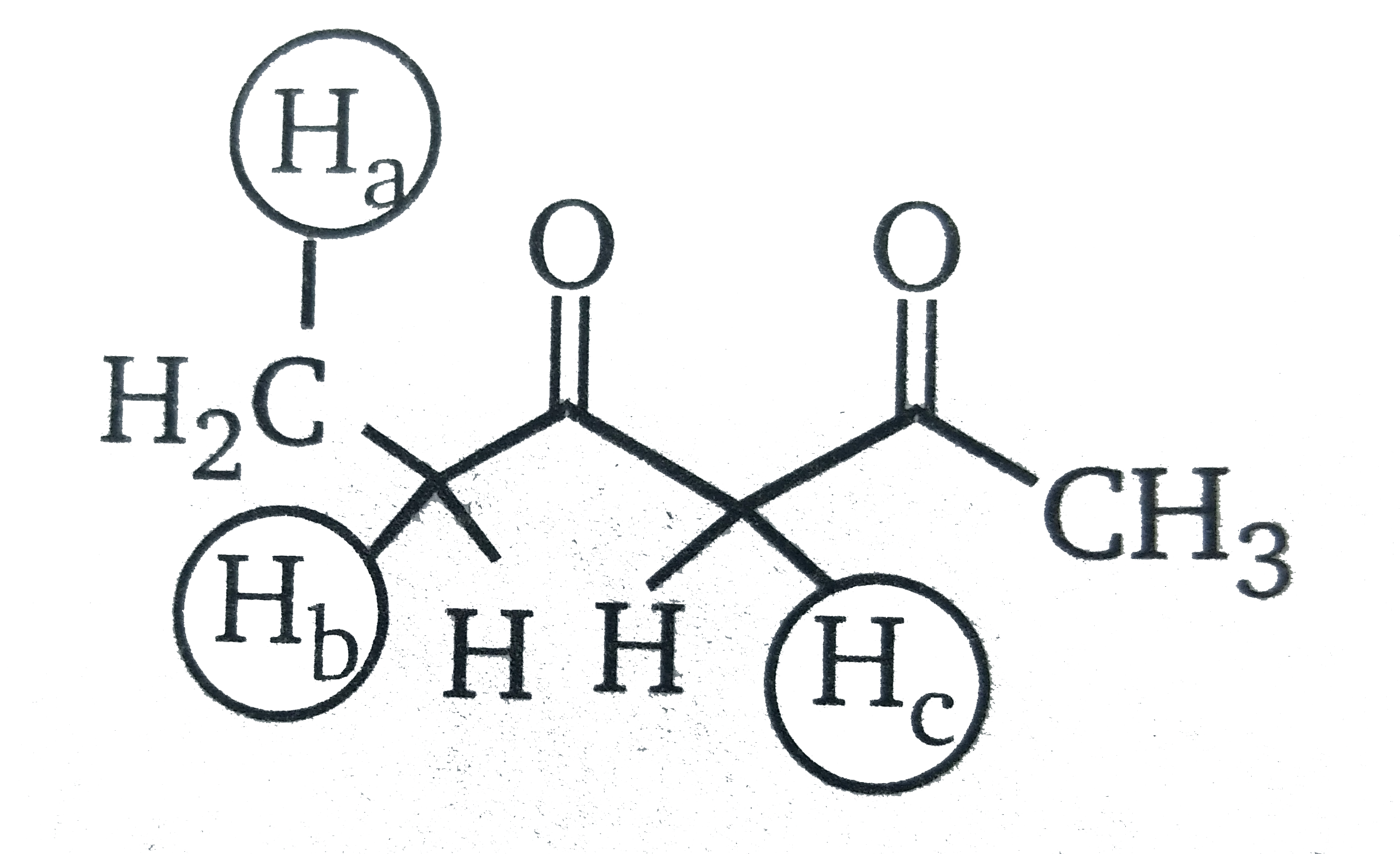A $a > b > c$
B $b > a > c$
C $b > c > a$
D $c > b > a$
Question 3 - Select One
Five molecules of a gas have speeds 1, 1, 3, 3, 2 km/s the value of the r.m.s spreed of the gas molecules is
A $\sqrt{\frac{4}{5}} k m / s$
B $\sqrt{\frac{23}{5}} k m / s$
C $\sqrt{\frac{24}{5}} k m / s$
D $\sqrt{\frac{87}{5}} k m / s$

NCERT EXEMPLAR-KINETIC THEORY-Multiple Choice Questions (MCQs)

Home
Ask Doubt
Profile