Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density p. Assume the velocity is along x-axis and the are of cross-section of the block perpendicular to v0 is A. show that the drag force on the block is 4rAv0√kTm where,m is the mass of the gas molecule.
Consider the digram

Let n = number of molecules per unit volume
Vrms= rms speed of the gas molecules
When block is moving with speed vo relative speed of molecules w.r.t. front face =v +vo where m = mass of molecule.
Number of collision in time Δt=12(v+vo)nΔtA, where A = area of croos- section of block and factor of 1/2 appears due to particles moving towards block.
∴ Momentum transferred in time Δt=m(v+v0)2nAΔt from front surface.
Similarly, momentum transferred in time Δt=m(v−V0)2nAΔt (from back suface)
∴Net force (drag force)=mnA[v+v0)2] [from front]
=mnA(4∨0)=(4mnAv)v0
=(4pAv)v0
Where we have assumed pmnV=mV
if v= velocity along x-axis
Then we can write KE=12mv2=12kBT
⇒ v=√kBTm ⎡⎢
⎢
⎢
⎢
⎢⎣[KB=Boltzmann constnatKE=Kinetic energyT=Temperature⎤⎥
⎥
⎥
⎥
⎥⎦
∴ From eq .(i). Drag force =(4pAv)v0=4pAv.√KBTmv0.
Topper's Solved these Questions
Similar Questions
Consider a rectangular block of wood moving with a velocity v0 in a gas at temperature T and mass density p. Assume the velocity is along x-axis and the are of cross-section of the block perpendicular to v0 is A. show that the drag force on the block is 4rAv0√kTm where,m is the mass of the gas molecule.
View SolutionA block of mass 2 kg is moving with a velocity of 2ˆi−ˆj+3ˆk m/s. Find the magnitude and direction of momentum of the block with the x-axis.
View Solution
Knowledge Check
- Question 1 - Select One
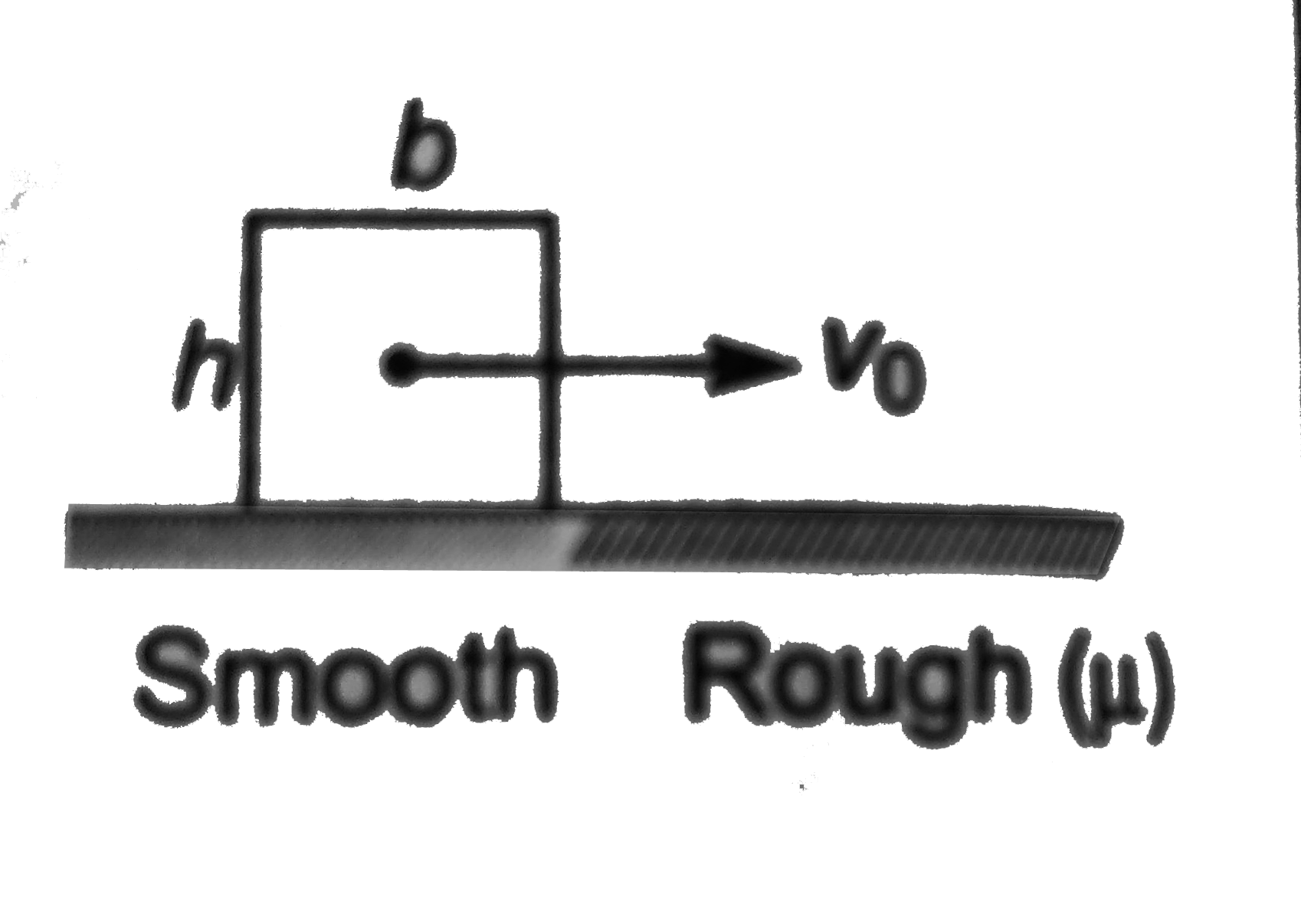
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.AThenet torque acting on the block about its COM is μmg(h)2 (clockwise)Bthe net torque acting on the block about its COM is zeroCThe net torque acting on the block about its COM is in the anticlockwise senseDNone of the above. - Question 2 - Select One
A bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 A√2ghBM+mm√2ghCmM+m2ghDM+mM√2gh
A√2ghBM+mm√2ghCmM+m2ghDM+mM√2gh - Question 3 - Select One
A bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 A√2ghBM+mm√ghCmM+m2ghDM+mM√2gh
A√2ghBM+mm√ghCmM+m2ghDM+mM√2gh
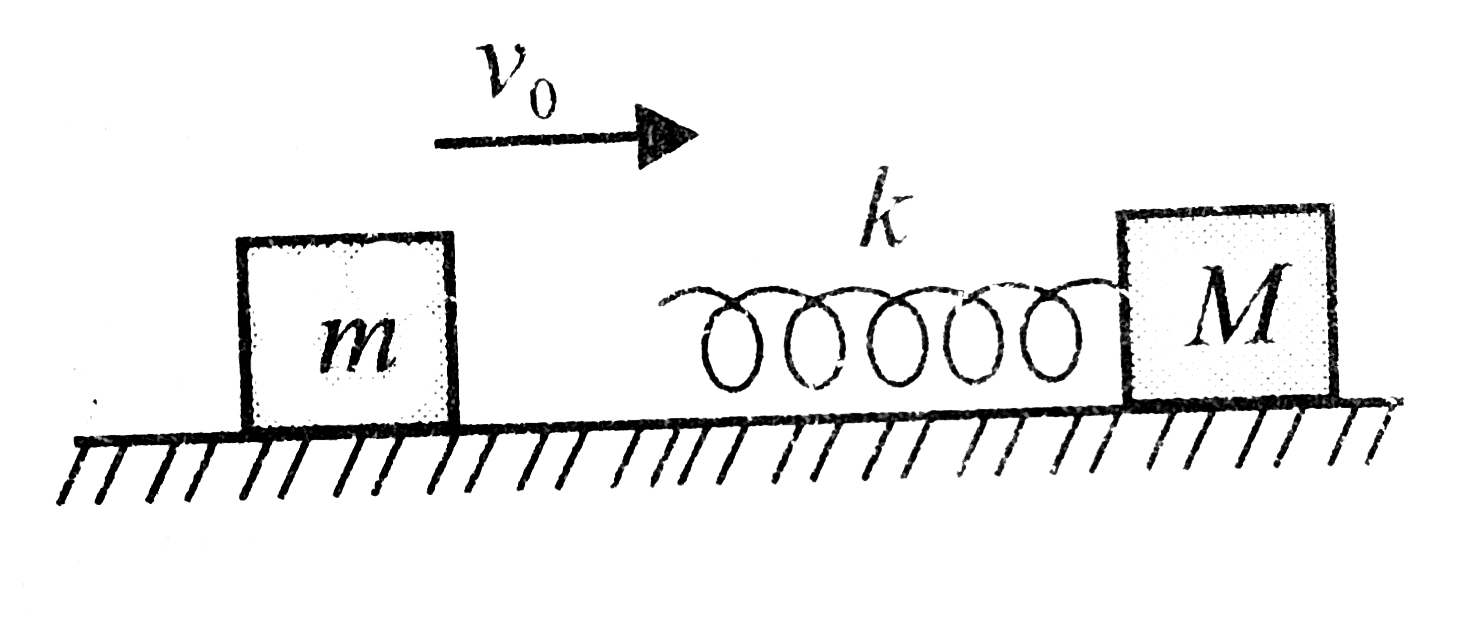
In the fig 4.24 a block of mass m moves with velocity v0 toward a stationaly block of a mass M on a smooth horizontal surface. Find the maximum compression in the spring of stiffnesss constant K.
 View Solution
View SolutionA block of mass m moving with a velocity v0 collides with a stationary block of mass M to which a spring of stiffness k is attached, as shown in Fig. Choose the correct alternative(s)
 View Solution
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 View Solution
View Solution

