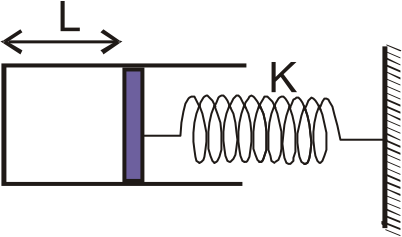
Consider one mole of perfect gas on a cylinder of units cross-section with a piston attched (figure). A spring (spring constant K ) is attched (unstrecthed lengthL ) to the piston and to the bottom of the cylinder . Inditially the spring is unstrecthed and the gas is in equailibrium. A certain amount of heat Q is supplied to the gas causing an increase of value from V0 to V1.
(a) What is the initial pressure of the system ?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamic, write down a relation between Q,pa,V,V0 and K.

(a) Initially the piston is in equilibrium hence,p9i)=pa
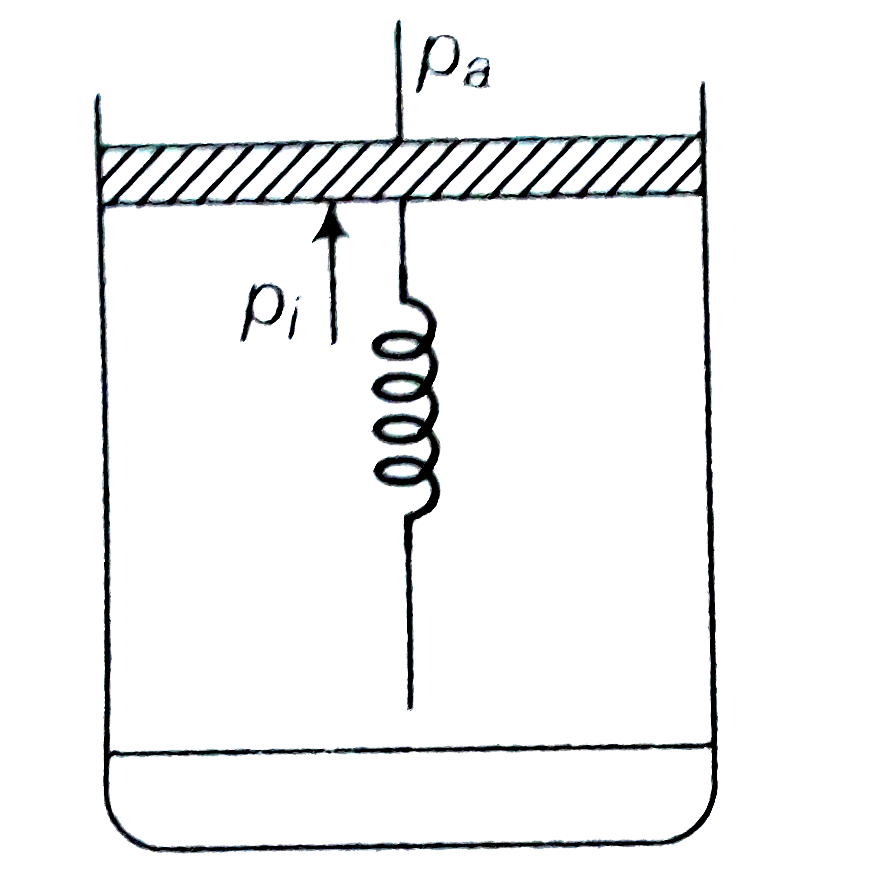
(b) On supplying heat, the gas expands form V0 to V1
∴ Increase in volume of the gas = V1−V0
x=V1−V0Area=V1−V0
∴ Force exerted by the spring on the piston
=F=kx=(V1−V0)
Hence, Final pressure =pf=pa+kx
=pa+k×(V1−V0)
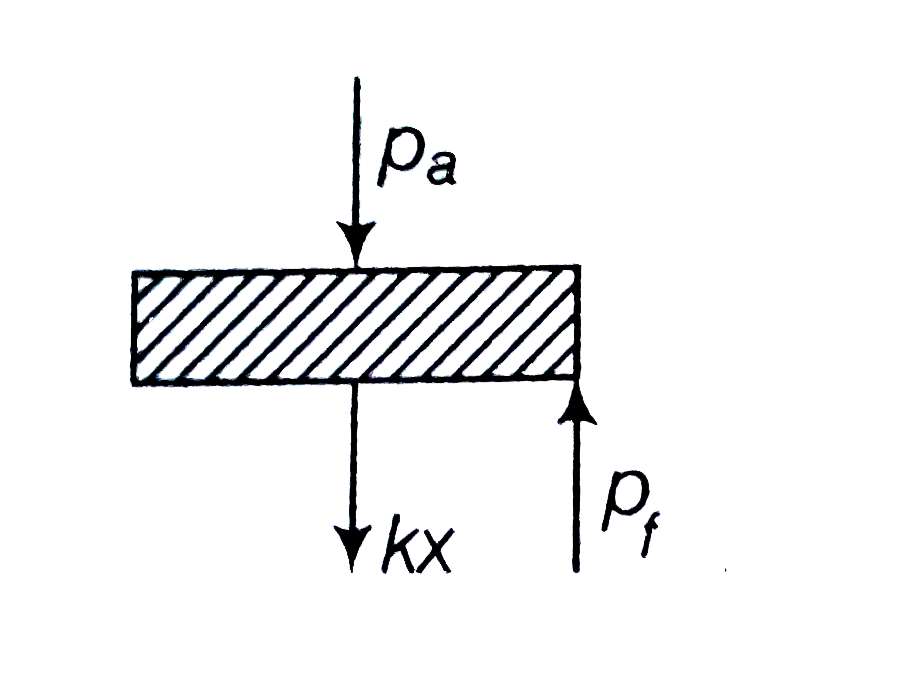
(c) From first law of therodynamics dQ = dU + dW
If T is final temperature of hte gas, then increase in the internal energy
dU=CV(T,T0)=Cv(,T0)
We can write , T=pfV1R=[pa+K(V1−V0)R]V1R
Work done by the gas = pdV + increase in PE of the spring
pa(v1−V0)+12kx2
Now, we can write dQ = dU + dW
Cv(T−T0)+pa(V−V0)+12kx2
=Cv(T−T0)+Pa(V−V0)+12(V1−V0)2
This is the required relation .
Topper's Solved these Questions
- THERMODYNAMICS BOOK - NCERT EXEMPLARCHAPTER - THERMODYNAMICS EXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLARCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
- UNITS AND MEASUREMENTS BOOK - NCERT EXEMPLARCHAPTER - UNITS AND MEASUREMENTS EXERCISE - Long Answer Type Questions
9 Videos
Similar Questions
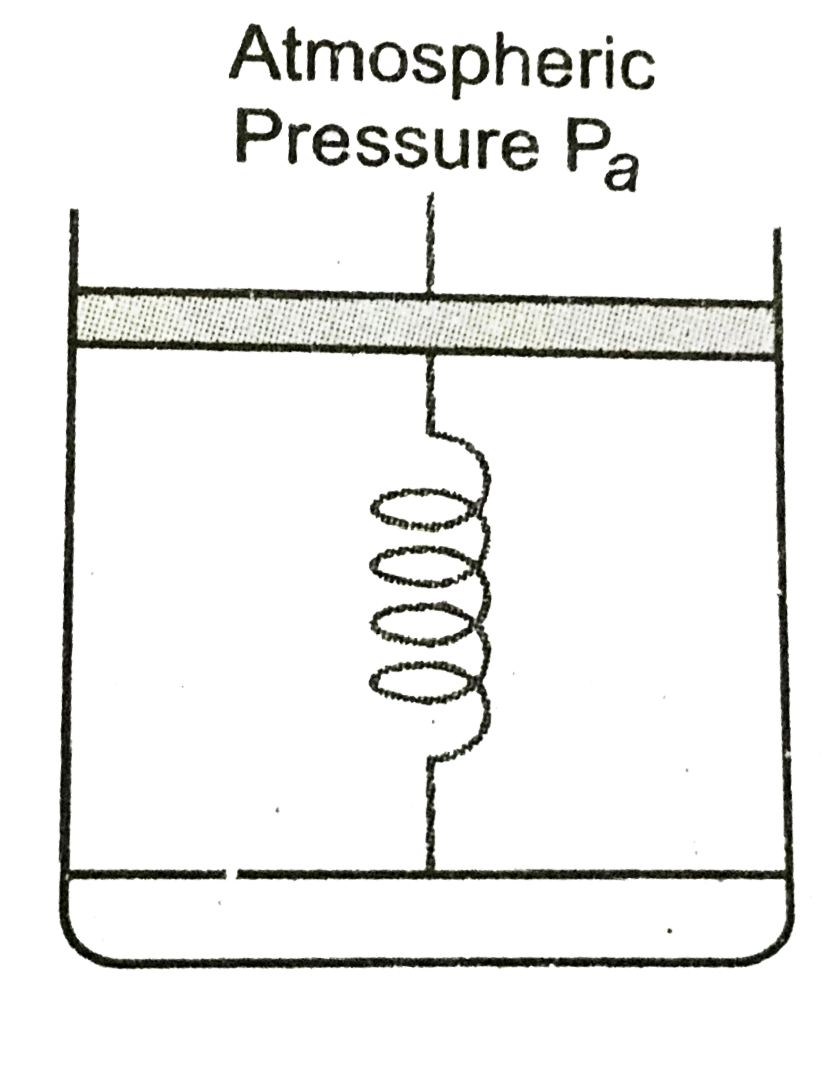
Consider one mole of a perfect gas in a cyclinder of unit cross section with a piston attached, (figure) A spring (spring constant K) is attached (unstretched length L) to the piston and the bottom of the cylinder. Initially, the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V0toV.
(a) What is the initial pressure of the system?
(b) What is the final pressure of the system?
(c) Using the first law of thermodynamics, write down a relation between Q,Pa,V,V0 and K.
View SolutionOne mole of a perfect gas in a cylinder fitted with a piston has a pressure P, volume V and temperature T. if the temperature is increased by 1K keeping pressure constant, the increase in volume is
View Solution
Knowledge Check
A metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
Ak=YA/LBk=2YA/LCk=YA/2LDk=YL/AIf a metal wire of length L, having area of cross-section A and young' s modulus Y . Behave as a spring of spring constant K. The value of K is
AYALBYA2LC2YALDYLAA solid sphere rolls without slipping and presses a spring of spring constant k as shown in figure. Then, the compression in the spring will be
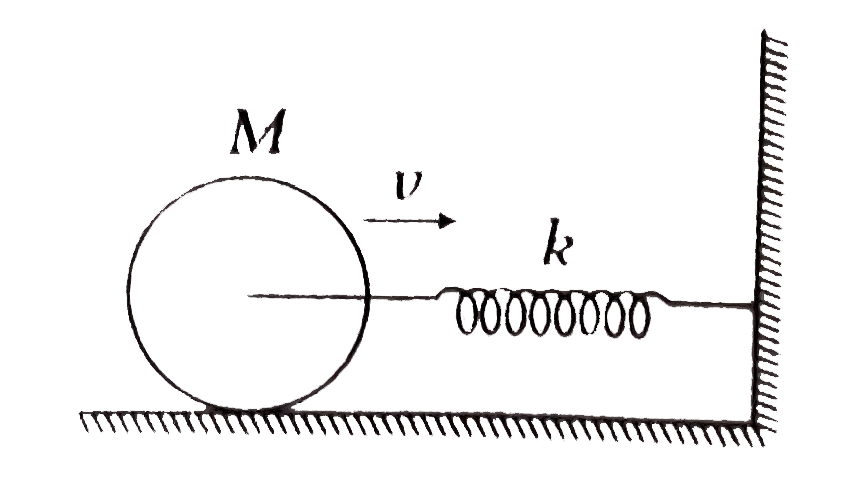 Av√2M3kBv√2M5kCv√5k7MDv√7M5k
Av√2M3kBv√2M5kCv√5k7MDv√7M5k
A horizontal cylinder has two sections of unequal cross - sections, in which two pistons can move freely. The pistons are joined by a string, Some gas is trapped between the pistons. If this gas is heated the pistons will

View SolutionMethod 3 of W
Mass of a piston shown in Fig. is m and area of cross-section is A. Initially spring is in its natural length. Find work done by the gas.

View SolutionA gas is contained in a metallic cylinder fitted with a piston.the piston is suddenly moved in to compress the gas and is maintained at this position. As time passes the pressure of the gas in the cylinder
View SolutionA fixed container is fitted with a piston which is attached to a spring of spring constant k. The other and of the spring is attached to a rigid wall. Initially the spring is in its natural length and the length of container between the piston and its side wall is L. Now an dideal diatomic gas is slowly filled in the container so that the piston moves quasistatically. It pushed the piston by x so that the spring now is compressed by x. The total rotaional kinetic energy of the gas molecules in terms of the displacement x of the piston is (there is vacuum outside the container)
View SolutionIn the arrangement shown in the fig the cylinder is insulating one. Both sides same diatomic gas is trapped by two insulting massless pistos with the help of an ideal spring. The natural length of the spring is equal to the length of the cylinder. initial state of the gases are as shown in the figure.

What is the value of energy stored in the spring ?
View Solution
