A manufacturer has three machines A,B and C installed in his factory. Machines A and B are capable of being operated for atmost 12 hours whereas machine C must be operated for atleast 5 hours a day. He produces only two items X and Y each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of X and Y on three machines are given in the following table:
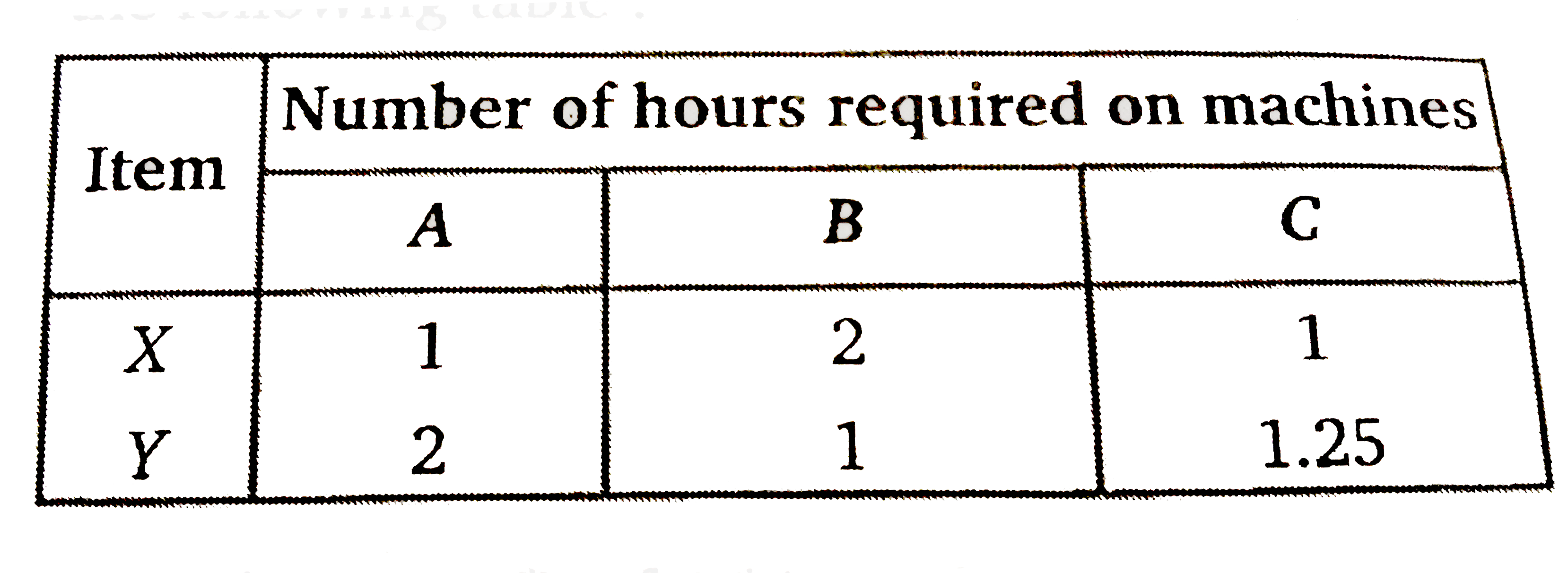
He makes a profit of Rs. 600 and Rs. 400 on each item of X and Y respectively. How many of each item should he produce so as to maximize his profit assuming that he can sell all the items that he produced?
The correct Answer is:Type X=4, Type Y=4
NA
Topper's Solved these Questions
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHANChapter:LINEAR PROGRAMMINGExercise:Exercise 12.1
Explore 10 Videos
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHANChapter:LINEAR PROGRAMMINGExercise:Exercise 12.2
Explore 11 Videos
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHANChapter:LINEAR PROGRAMMINGExercise:Exercise 12 A
Explore 8 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBook:NAGEEN PRAKASHANChapter:INVERES TRIGONOMETRIC FUNCTIONSExercise:Miscellaneous Exercise (prove That )
Explore 9 Videos
- MATRICESBook:NAGEEN PRAKASHANChapter:MATRICESExercise:Miscellaneous Exerice
Explore 15 Videos
Similar Questions
Maximise Z=3x+4y
Subject to the constraints
x+y≤4,x≥0,y≥0
View SolutionReshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contain at leat 8 units of vitamin A and 11 units of vitamin B. Food P cost Rs. 60/kg and Food Q costs Rs. 80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of Vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
View SolutionSolve the following linear programming problem graphically:
Maximize : z=60x+15y
Subject to : x+y≤50
3x+y≤90
x≥0
y≥0
View SolutionProve that:tan−1√x=12cos−1(1−x1+x),x∈[0,1]
View SolutionLet A=[0100]show that (aI+bA)n=anI+nan−1bA, where I is the identitymatrix of order 2 and n∈N.
View Solution(Manufacturing problem) A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine HI must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of M and N on the three machines are given m the following table:She makes a profit of Rs 600 and Rs 400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rsl7.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
View SolutionA manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs. 7 profit and that of B at a profit of Rs. 4. Find the production level per day for maximum profit graphically.
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
View SolutionA manufacturer has 3 machines I, II and III installed in his factory. Machines I and II are capable of being operated for utmost 12 hours whereas machine III must be operated atleast for 5 hours a day. He produces only two items A and B each requiring the use of three machines. The number of hours required for producing 1 unit of each of the items A and B on the three machines are given below.

He makes a profit of Rs 7600 on item A and Rs 400 on item B. Assume that he can sell all that he produces.
(i) Formulate this as a linear programming problem.
(ii) Solve the L.P.P by corner point method.
View Solution(Manufacturing problem): A manufacturer has three machines. I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the sue of all the three machines.
The number of hours required for producing 1 unit of each of M and N on the three machies are given in the follownig table:

She makes a profit of Rs. 600 and Rs. 400 on items M and N respectively. How many of each item should be produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
View Solution(Manufacturing problem): A manufacturer has three machines. I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the sue of all the three machines.
The number of hours required for producing 1 unit of each of M and N on the three machies are given in the follownig table:

She makes a profit of Rs. 600 and Rs. 400 on items M and N respectively. How many of each item should be produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machine for at most 12 hours a day?
View SolutionA manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs. 7 profit and that of B at a profit of Rs. 4. Find the production level per day for maximum profit graphically.
View SolutionA furniture form manufactures chairs and tables, each requiring the use of three machines A, B and C. Production of one chair requires 2 hours on machine A, 1 hour on machine B, and 1 hour on machine C. Each table requires 1 hour each on machines A and B and 3 hours on machine C. Profit realized by selling one chair is Rs. 30 while for a table the figure is Rs. 60. The total time available per week on machine A is 70 hours, on machine B is 40 hours, and on machine C is 90 hours. How many chairs and table should be made per week so as to maximize profit? Develop a mathematical formulation.
View Solution
