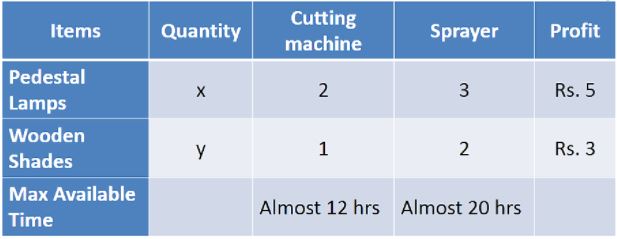
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at die most 12 hours. The profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
Let the number of pedestal lamps be x
and the number of wooden shades be y
Cutting Machine
Time on Pedestal lamps → 2 hrs
Time on Wooden shades → 1 hrs
Maximum Time → atmost 12 hrs
∴
2x+y≤12
x,y≥0
Sprayer
Time on Pedestal lamps → 3 hrs
Time on Wooden shades → 2 hrs
Maximum Time → atmost 20 hrs
∴
3x+2y≤20
x,y≥0
As, we want to maximize the profit, hence the function used here is Maximize Z
Profit on Pedestal lamps → Rs 5
Profit on wooden shades → Rs 3
Maximize Z=5x+3y
Combining all Constraints:
Maximize Z=5x+3y
Subject to Constraints
2x+y≤12
3x+2y≤20
x≥0,y≥0
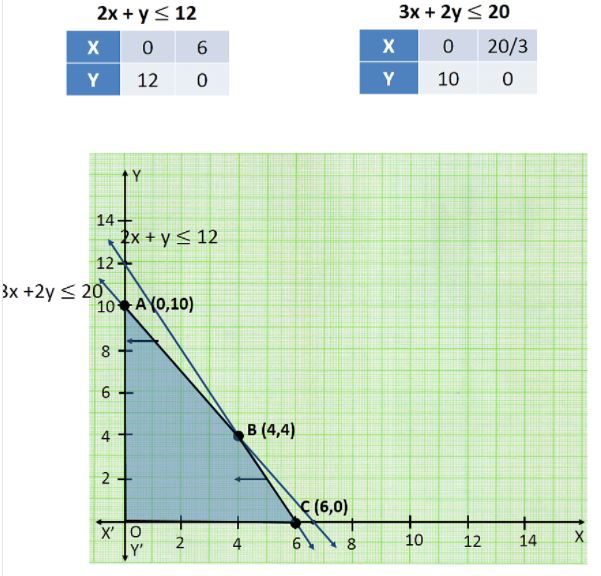

∴ The profit will be maximum if,
Number of lamps → 4
Number of Wooden Shades → 4
Maximum profit → Rs 32
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - LINEAR PROGRAMMINGEXERCISE - SOLVED EXAMPLES11videos
LINEAR PROGRAMMING
- BOOK - NCERTCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise10videos
LINEAR PROGRAMMING
- BOOK - NCERTCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE17videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.312videos
MATRICES
Similar Questions
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/ cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lam. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hour and the grinding/ cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade isRs. 3. Assuming that the manufacturer can sell all the lamps and shades that the produces how should be scehdule his daily production in order to maximise his profit?
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 25 and that from a shade is Rs. 15. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit. Formulate an LPP and solve it graphically.
View Solution
Knowledge Check
- Question 1 - Select One
Scent sprayer is based on
ABernoulli's theoremBCharles's lawCBoyal's lawDArchimedes principle - Question 2 - Select One
A manufacturer produces two types of soaps using two machines A and B . A is operated for 2 minutes and B for 3 minutes to manufacture first type , while it takes 3 minutes on machine A and 5 minutes on machine B to manufature second type . Each machine can be operated at the most for 8 hours per day . The two types of soap are sold at a profit of Rs 0.25 and Rs 0.05 each respectively . Assuming that the manufactured can sell all the soaps he can manufacture , how many soaps of each type should be manufature per day so as to maximize his profit .
A50 soaps of type I , 20 soaps of types IIB96 soaps of type IIC45 soaps of type ID55 soaps of type I
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and a sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes one hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs. 5 and that from a shade is Rs. 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Make an L.P.P. and solve it graphically.
View SolutionA cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and 2 hours on the sprayer to manufacture a shade.On any day, the sprayer is available for at the most 12 hours and the grinding/cutting machine for at the most 12 hours.The profit from the sale of a lamp is ₹ 5 and that from a shade is ₹ 3.Assuming that manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package on screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacturer a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs. 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day order to maximise his profit? Determine the maximum profit.
View SolutionA factory manufatures two types pf screws A and B, Each type of screw requires the use of two machines, an automatic and a hand operated.It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B.Each machine is available for at the most 4 hours on any day.The manufacturer can sell a package of screws A at a profit of ₹ 7 and screws B at a profit of ₹ 10.Assuming that he can sell all the screws he amnufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit?Determine the maximum profit.
View SolutionA manufacture produces two types of soap bars using two machines, A and B.A is operated for 2 minutes and B for 3 minutes to manufacture the first type, while it takes 3 minutes on machine A and 5 minutes on machine B to manufacture the second type. Each machine can be operated at the most for 8 hours per day. The two types of soap bars are sold at a profit of R. 0.25 and Rs 0.50 each. Assuming that the manufacture can sell all the soap bars he can manufacture, hwo many bars of soap of each type should be manufactured per day so as to maximize his profit ?
View Solution

