A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package on screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacturer a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs. 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day order to maximise his profit? Determine the maximum profit.
Let the manufacturer makes packets of screw and packets of screw B per day. Then

Maximise ………………1
and constraints
…………………2
.....................3
and
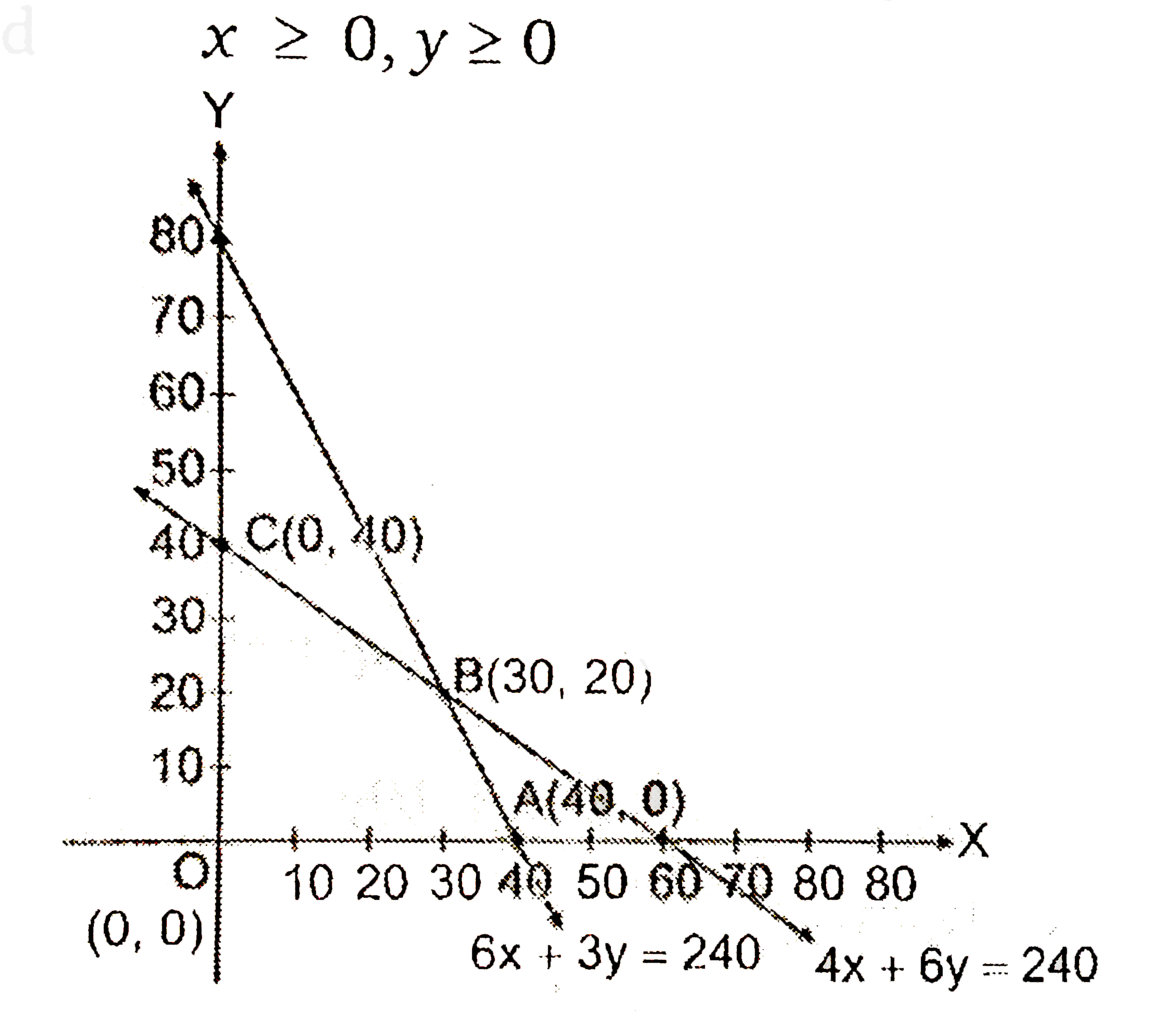
First draw the graph of the line
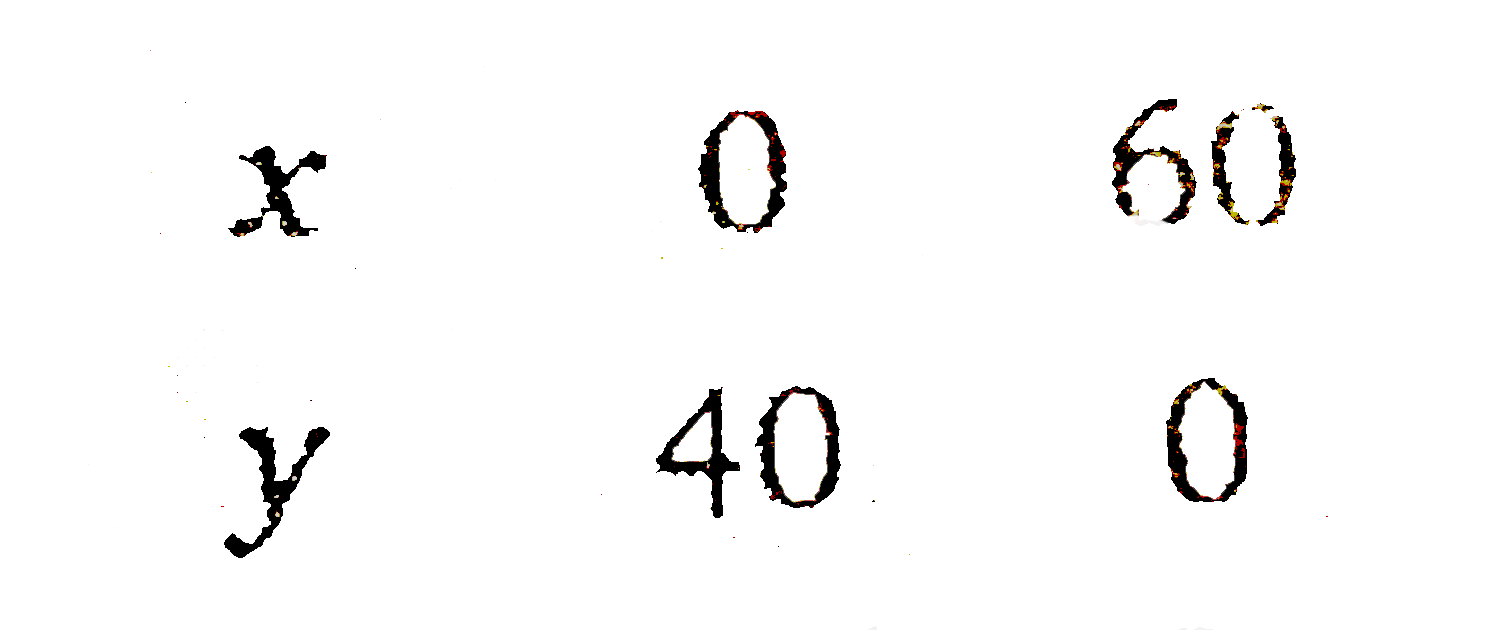
Put in the inequation
(True)
Therefore, half plane contains the origin,
Now draw the graph of the line
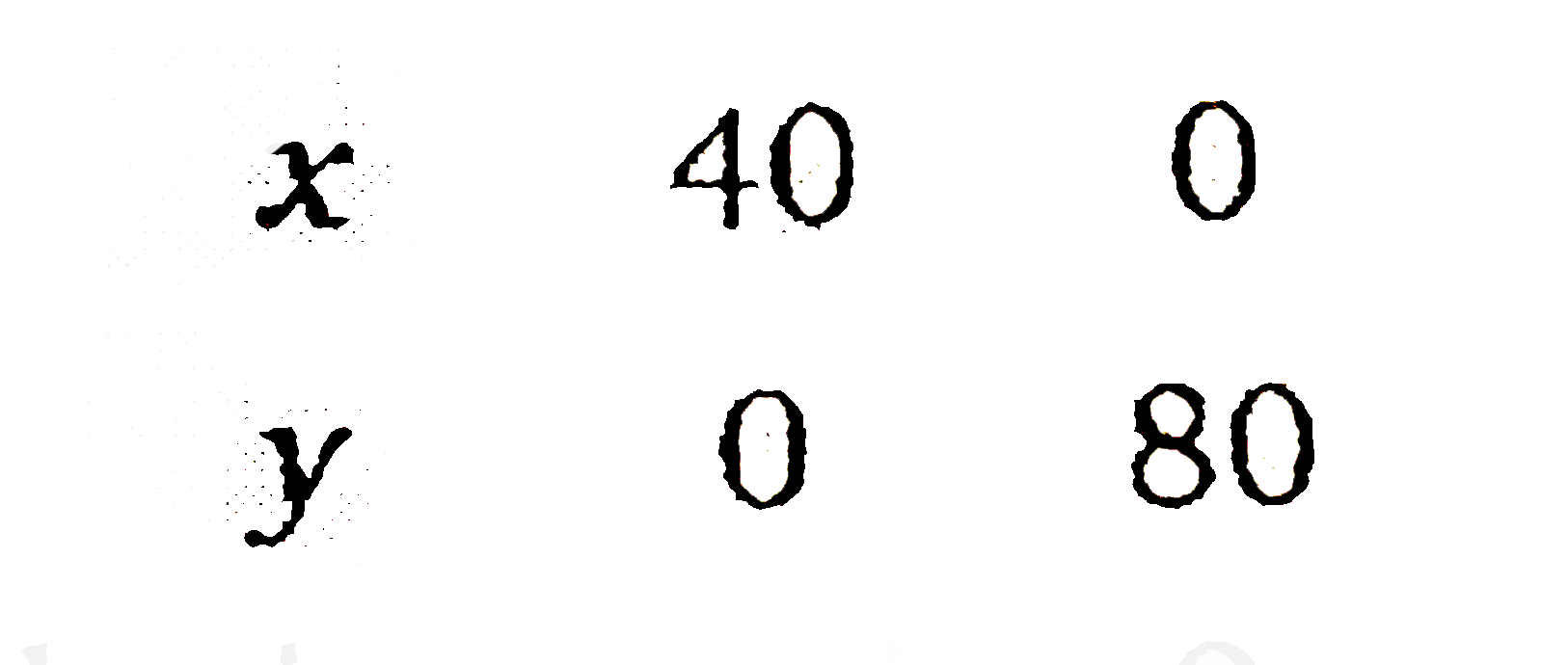
Put in the inequation
(True)
Therefore half plane contains the origin.Since, . So the feasible region will be in first quadrant.
From equations and the point of intersection is .
Feasible region is OABCE.
The vertices of the feasible region are and we find the value of at these points.
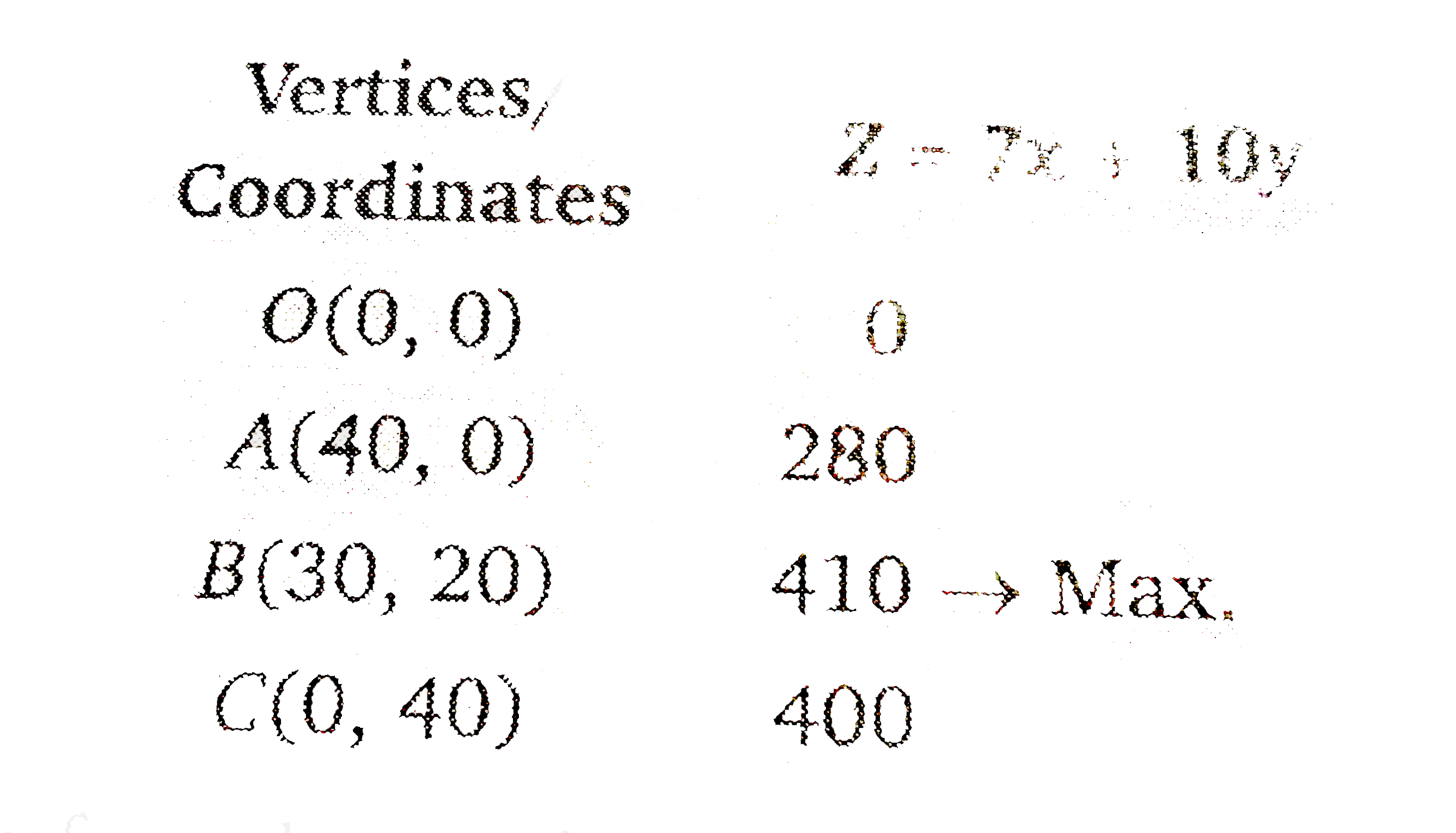
Therefore, the maximum value of is Rs. 410 at point . Therefore, the maximum profit of Rs. 410 will be obtained when the factory produces 30 packets of screw A and 20 packets of screw B per day.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Miscellaneous Exercise
9 Videos
- LINEAR PROGRAMMINGBOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12.1
10 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )
9 Videos
- MATRICESBOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice
15 Videos
Similar Questions
A factory manufatures two types pf screws A and B, Each type of screw requires the use of two machines, an automatic and a hand operated.It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B.Each machine is available for at the most 4 hours on any day.The manufacturer can sell a package of screws A at a profit of ₹ 7 and screws B at a profit of ₹ 10.Assuming that he can sell all the screws he amnufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit?Determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View Solution
Knowledge Check
A manufacturer produces two types of soaps using two machines A and B . A is operated for 2 minutes and B for 3 minutes to manufacture first type , while it takes 3 minutes on machine A and 5 minutes on machine B to manufature second type . Each machine can be operated at the most for 8 hours per day . The two types of soap are sold at a profit of Rs 0.25 and Rs 0.05 each respectively . Assuming that the manufactured can sell all the soaps he can manufacture , how many soaps of each type should be manufature per day so as to maximize his profit .
A50 soaps of type I , 20 soaps of types IIB96 soaps of type IIC45 soaps of type ID55 soaps of type I
A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B, each type requiring the use of two machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on hand-operated machines to manufacture a packet of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machines to manufacture a packet of screws 'B'. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a packet of screws 'A' at a profit of 70 paise and screws 'B' at a profit of Rs. 1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximise his profit ? Formulate the above L.P.P. and solve it graphically and find the maximum profit.
View SolutionA manufacture produces two types of soap bars using two machines, A and B.A is operated for 2 minutes and B for 3 minutes to manufacture the first type, while it takes 3 minutes on machine A and 5 minutes on machine B to manufacture the second type. Each machine can be operated at the most for 8 hours per day. The two types of soap bars are sold at a profit of R. 0.25 and Rs 0.50 each. Assuming that the manufacture can sell all the soap bars he can manufacture, hwo many bars of soap of each type should be manufactured per day so as to maximize his profit ?
View SolutionA company manufactures two types of screws A and B. all the screws have to pass through a threading machine and a slotting machine. A box of type A screw requires 2min on the threading machine and 3 min on the slotting machine. A box of type B screw requires 8 min on the threading machine and 2 min on the slotting machine. In a week each machine is availbale for 60h. On selling these screws, the company gets a profit of 100 box on type A screw and 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
View SolutionA company manufactures two types of screws A and B. all the screws have to pass through a threading machine and a slotting machine. A box of type A screw requires 2min on the threading machine and 3 min on the slotting machine. A box of type B screw requires 8 min on the threading machine and 2 min on the slotting machine. In a week each machine is availbale for 60h. On selling these screws, the company gets a profit of 100 box on type A screw and 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
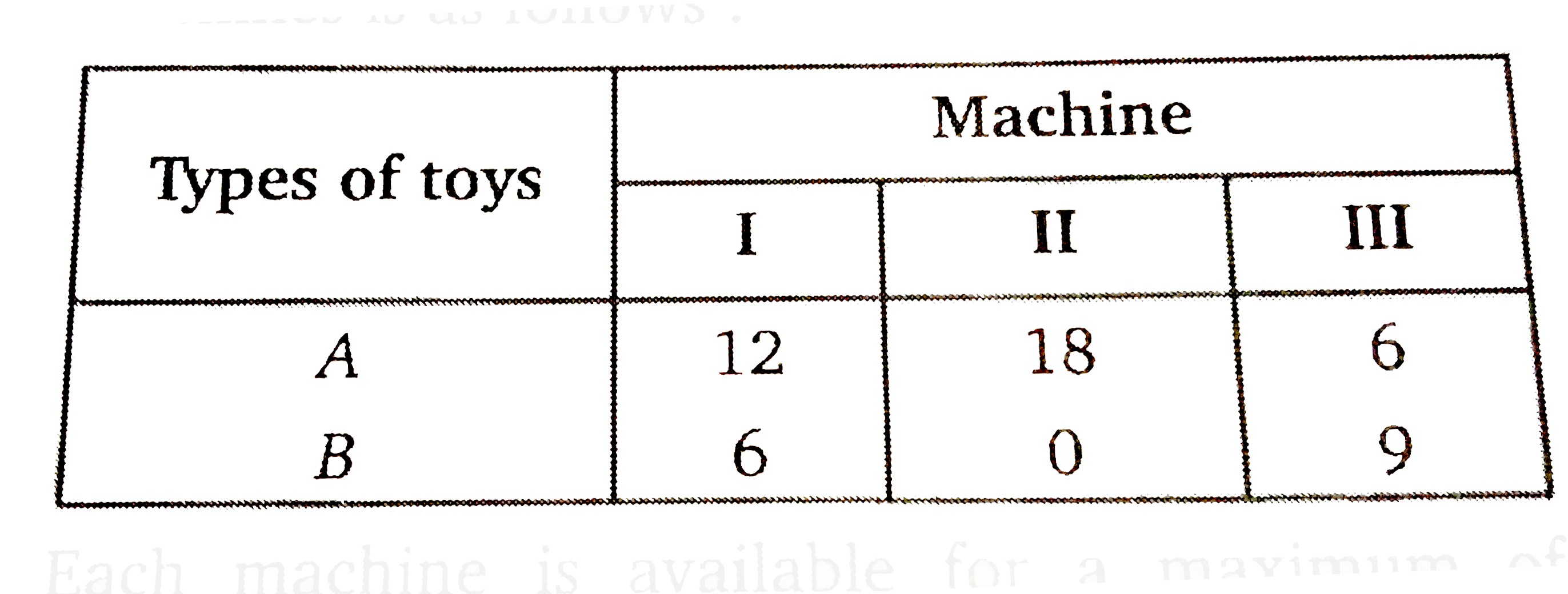 Each machine is available for a
maximum of 6 hours per day. If the profit
Each machine is available for a
maximum of 6 hours per day. If the profit
View Solution
