On a common hypotenuse AB, two right angled triangles, ACB and ADB are situated on opposite sides. Prove that ∠BAC=∠BDC.
Given, ΔACBandΔADB are two right angled triangles with common hypotenuse AB.
To prove ∠BAC=∠BDC
Construction join CD.
Proof Let O be the mid-point of AB.
Then, OA=OB =OC=OD.
Since, mid-point of the hypotenuse of a right triangle is equidistant from its vertices. Now, draw a circle to pass through the points A, B, C and D. with O as centre and radius equal to OA.
We know that, angles in the same segment of a circle are equal. From the figure, ∠BACand∠BDC are angles of same segment BC.
∴∠BAC=∠BDC

Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
A point D is taken from the side BC of a right angled triangle ABC, where AB is hypotenuse. Then,
AAB2+CD2=BC2+AD2BCD2+BD2=2AD2CAB2+AC2=2AD2DAB2+AD2=BD2
Show that in a right angled triangle, the hypotenuse is the longest side.
View SolutionProve that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
View SolutionA side of an isosceles right angled triangle is x. Find its hypotenuse.
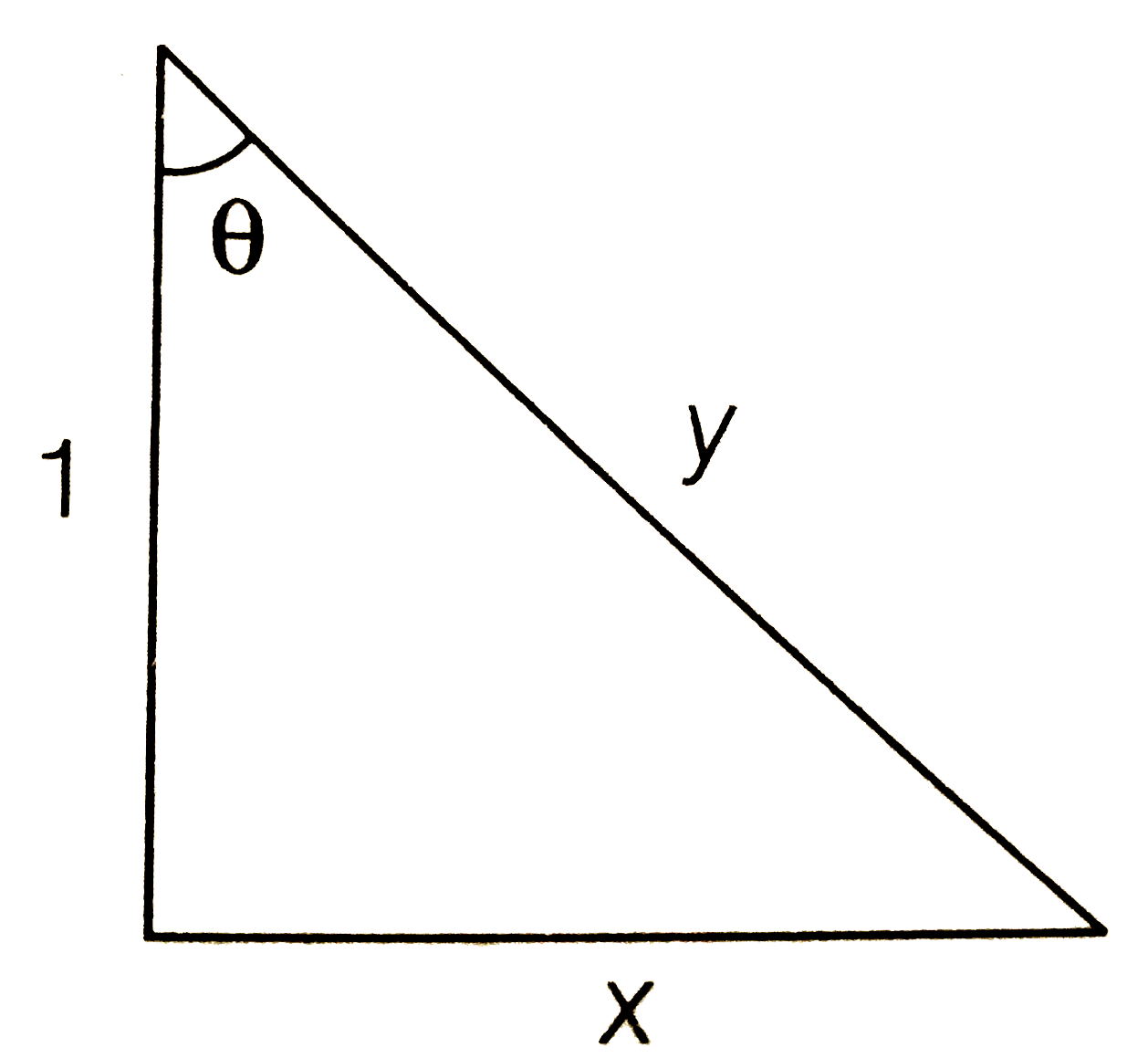
View SolutionA right angled triangle has legs 1 and x. The hypotenuse is y and angle opposite to the side x is θ. Shown as

View SolutionFind the length of the hypotenuse in a right angled triangle where the sum of the squares of the sides making right angle is 169.
View SolutionIn a right angled triangle with sides a and b and hypotenuse c , the altitude drawn on the hypotenuse is x . Prove that ab=cx .
View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View Solution
