Two circles whose centres are and intersect at Through a line parallel to intersecting the circles at is drawn. Prove that
Given, draw two circles having centres O and O' intersect at points A and B.
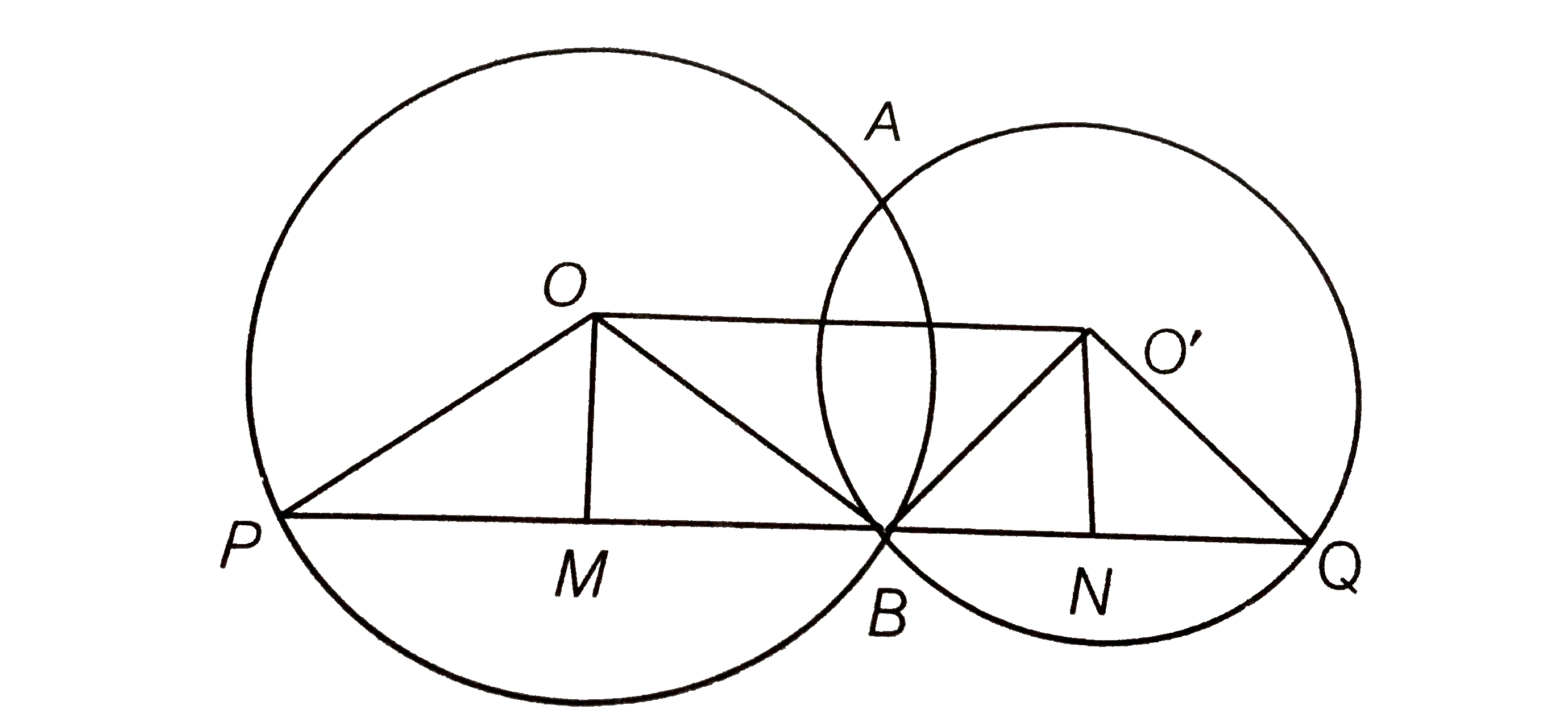
Also, draw line PQ parallel to OO'.
Construction Join OO', OP, O'Q, OM and O'N.
To prove PQ=2OO'
Proof In [OM is the perpendicular bisector of PB]
and in [O' N is the perpendicular bisector of BQ]
[adding both sides BM+BN]
=BP+BQ=PQ
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.42videos
CIRCLES
- BOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles34videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two circles of same radius r centred at O and O' touch each other at P as shown in the figure, if OO' is produced to meet the circle C(O'r) at A and AT is a tangent to the circle C(O,r) such that O'Q ⊥ AT . Then AO : AO'=
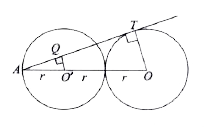 A32B2C3D14
A32B2C3D14
The diagonals of a parallelogram ABCD intersect at OA line through O intersects AB at XandDC at Y Prove that OX=OY
View SolutionThe diagonals of a parallelogram ABCD intersect at O.A line through O intersects AB at X and DC at Y. Prove that OX=OY.
View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP =∠QCD.
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
 View Solution
View SolutionIn the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.
 View Solution
View SolutionThe circumferences of three unequal circles whose centres are A, B and C pass througha common point, O, from which lines are drawn through A, B and C meeting the circumferences at A', B' and C". Show that the sides of ΔA'B'C' pass through the other points of intersection of the circles and are respectively parallel to the sides of the ΔABC
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
View Solution

